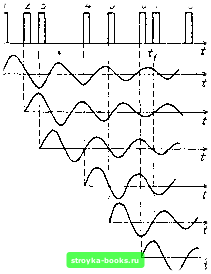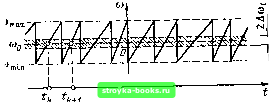Рис. 7.11. Отклики колебательной цепи на отдельные импульсы хаотической последовательности

Рис. 7.12. Изменение частоты колебания по пилообразному закону со случайным периодом

релированы, а между фазами составляющих из различных спектров никакой корреляции нет (из-за случайной расстановки импульсов на оси времени). Чем уже полоса прозрачности контура, тем меньшую роль играет корреляция фаз в парциальных спектрах.

Приведем другой пример, поясняющий явление нормализации в узкополосной цепи. Пусть на контур воздействует непрерывное колебание с по-стоянйой амплитудой и с частотой, модулированной по пилообразному закону со случайным периодом (рис. 7.12). При каждом пробеге частоты через полосу прозрачности контура 2Дюо в последнем возникает свободное колебание, амплитуда которого обратно пропорциональна наклону «пилы». Так как моменты пересечения полосы прозрачности расположены на оси времени случайнььм образом, то и свободные колебания образуют импульсную последовательность со случайными интервалами (t, th+i)-

При медленном качании частоты, когда интервалы велики по сравнению с постоянной времени контура т„, свободные колебания не перекрываются. Предположим, что т„ велико по сравнению со средним значением интервалов Грр.Тогда в любой момент времени будет накладываться много колебаний со случайными и взаимно независимыми фазами и амплитудами. При этом входное колебание, закон распределения которого определяется формулой (4.25) (изменение мгновенной частоты не отражается на одномерном законе распределения высокочастотного колебания с постоянной амплитудой), преобразуется в случайную функцию с распределением, близким к нормальному. Нормализация будет тем полнее, чем больше т„ по сравнению

Учитывая, что для одиночного контура имеет место соотношение AcdqTh = = 1, а средняя частота «пилы» Fp = I/Tcp- условие нормализации можно записать в форме неравенства fp > Ашо-

В широкополосных линейных цепях при некоторых условиях может иметь место эффект, обратный описанному выше эффекту нормализации: распределение процесса на выходе цепи может отличаться от нормального распределения больше, чем на входе. Можно привести простой пример подобного эффекта.

Пусть на вход дифференцирующего устройства подается совокупность относительно длинных импульсов, имеющая распределение, близкое к нормальному. В результате дифференцирования каждый из импульсов превращается на выходе в пару очень коротких импульсов, соответствующих фронтам входного импульса. Число взаимно перекрывающихся импуль-

сов на выходе уменьшается, благодаря чему приближение к нормальному закону на выходе оказывается худшим, чем на входе. Подобный эффект иногда называют «денормализацией» процесса.

Следует подчеркнуть, что отмеченный эффект не противоречит тому, что в любой линейной цепи гауссовский процесс сохраняет нормальный закон распределения. Если в приведенном выше примере среднее число импульсов в единицу времени довести до бесконечности (что необходимо для получения строго нормального распределения), то при дифференцировании, которое можно осуществить в физически реализуемой цепи, процесс будет гауссовским также и на выходе цепи.

Глава 8. НЕЛИНЕЙНЫЕ ЦЕПИ И МЕТОДЫ ИХ АНАЛИЗА

8.1. НЕЛИНЕЙНЫЕ ЭЛЕМЕНТЫ

Основные радиотехнические преобразования осуществляются с помощью либо нелинейных цепей, либо линейных цепей с переменными параметрами. Однако последние реализуются тоже с помощью нелинейных элементов (например, емкость /?-п-перехода в полупроводниковом диоде), а некоторые параметрические цепи сами работают в существенно нелинейном режиме (например, параметрический генератор). Приведем примеры некоторых нелинейных элементов.

Следует различать резистивные (сопротивления) и реактивные (индуктивности, емкости) нелинейные элементы.

Для радиотехнических цепей и устройств наиболее характерными и распространенными резистивными нелинейными элементами являются полупроводниковые, ламповые и любые другие приборы, используемые для усиления или преобразования сигналов и имеющие нелинейную вольт-амперную характеристику. Важным параметром резистивного нелинейного элемента является крутизна его характеристики.

Различают два следующих определения крутизны характеристики: а) в рассматриваемой рабочей точке при слабом сигнале (дифференциальная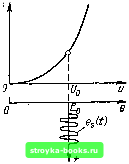

Рис. 8.1. Линейный режим работы элемента с нелинейной вольт-амперной характеристикой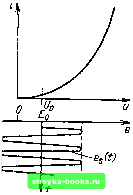

Рнс. 8.2. Нелинейный режим работы эле-цеита с той же вольт-амперной характеристикой, что и иа рис. 8.1

крутизна) и б) при Сильном гармоническом колебании (средняя крутизна).

С первым определением крутизны, соответствующим линейному режиму работы прибора (рис. 8.1), мы имели дело в гл. 5, где эта крутизна определялась выражением [см. (5.30), (5.33)] вида

(8.1)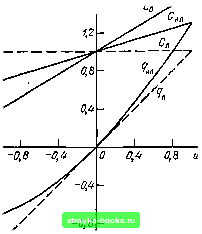

Рис. 8.3. Вольт-кулонная и вольт-фарад-ная характеристики линейной и иели-иейной емкостей

а напряжение Uq приравнивалось Ub3o (для транзистора).

Второе определение крутизны соответствует существенно нелинейному режиму работы устройства (рис. 8.2) и может быть дано лишь при учете формы вольт-амперной характеристики нелинейного элемента в широких пределах, зависящих от амплитуды входного сигнала (это будет сделано в § 8.5).

Примером нелинейной емкости может служить любое устройство с нелинейной вольт-кулонной характеристикой q (и).

На рис. 8.3 изображены вольт-кулонная (и) и вольт-фарадная характеристики С„л = (и)/и нелинейной емкости и аналогичные характеристики (и) и С„ = q„ (и)/и = const для линейной емкости. Вольт-кулонная характеристика нелинейной емкости в рассматриваемом примере была задана выражением дл (") = г"* при bi = 1 Кл/В н =

= 0,3 Кл/В В дальнейшем нелинейная емкость будет обозначаться С (и).

Если приложенное к емкости С (и) напряжение изменяется во времени, то ток через емкость можно определить с помощью одного из двух эквивалентных выражений

i{t):

dq (и) dq (и) du

dt dt dt

dC(u) du

du dt

(8.2) (8.3)

Если напряжение и = Uq + e, где Uo - напряжение в рабочей точке, а е-изменение напряжения, причем е С о. то емкость можно представить в виде

С„«£мМ. . (8.4)

du u=Uo

Определенную таким образом емкость иногда называют дифференциальной.

Параметр Со определяется крутизной вольт-кулонной характеристики (и). Показанная на рис. 8.3 зависимость Со от и определялась по формуле

Со= fei + 2b2«l„=t/. = l + 2-0,3i;o.

Наконец, катушка с ферромагнитным сердечником, обтекаемая сильным током, доводящим сердечник до магнитного насыщения, является примером нелинейной индуктивности L (i).