
 |
|
Главная Цепи и сигналы [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [ 74 ] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] Кусочно-линейная аппроксимация особенно проста и удобна для исследований и расчетов, когда основное значение имеет нижний сгиб характеристики, т. е. когда можно ограничиваться двумя прямыми (рис. 8.7, а). При более сложной форме используемого участка характеристики число аппроксимирующих отрезков растет и кусочно-линейная аппроксимация теряет свои преимущества. В подобных случаях иногда для аппроксимации применяются различные трансцендентные функции, например гиперболический тангенс, экспоненциальные функции и некоторые другие. Описанные выше приемы аппроксимации применимы и к соответствующим характеристикам реактивных нелинейных элементов. 8.3. ВОЗДЕЙСТВИЕ УЗКОПОЛОСНОГО РАДИОСИГНАЛА НА БЕЗЫНЕРЦИОННЫЕ НЕЛИНЕЙНЫЕ ЭЛЕМЕНТЫ Под безынерционным нелинейным элементом подразумевается любой электроннш прибор с нелинейной вольт-амперной характеристикой при использовании его в диапазоне частот, на которых можно пренебречь влиянием паразитных параметров (внутренних емкостей и индуктивностей). Рассмотрим режим работы, представленный на рис. 8.8, при котором напряжение сигнала (t) не выходит за пределы точки Ui и вольт-амперная характеристика i (и) удовлетворительно аппроксимируется степенным полиномом (8.8). Сигнал Bs (t) зададим сначала в форме гармонического колебания (t) = Е cos {(i>it + 0i) = Е cosi5i (t). Результаты анализа затем будут распространены на некоторые узкополосные радиосигналы. Подставив в (8.8) и - Ug = Cs (t), получим i (t) = ( (Ug) + Qi £ cos (/) + Qa COS (0 + 3 £ cos rpi(t) + ... (8.15) Форма тока i (t) показана на рис. 8.8. С помощью тригонометрических соотношений cosx---1--cos2x, cosx 3 - cosx-l--cos3x, cos*x = = - -f - COS 2x-\-- cos 4x, cos x= - cos x - -cos 3x -\- -{--COsSx и т.д. выражение (8.15) приводим к виду /(0 = аЕ + + -j-a,E + ..}j cosyPiit)+ll-ChE+ -i-a. £* + ••.) cos 2i;i (О + -f (-1-Оз£+ a, E+...у OS 3Pi it) + (-j«4£*-f ...)cos4i;i(0 + P + ... j cos Sifi (/) + ...=/„ 4 11 cos (0 + /3 cos 2i5i (0 + + /3 cos Зг), (/) + ... (8.16) Из этого выражения видны следующие проявления нелинейности вольт-амперной характеристики при гармоническом воздействии: 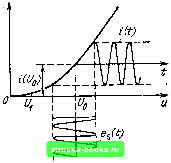 £ I t" Рис. 8.8. Слабонелинейный режим работы усилительного прибора ТОК покоя i (Uo) получает приращение, обусловленное коэффициентами а, а, ... при четных степенях полинома (8.8): lo=i(Uo) + -{hE+ а,Е* + ...; (8.17) амплитуда гармоники основной частоты ©1 связана с амплитудой возбуждения Е нелинейным соотношением, обусловленным нечетными степенями полинома (8.8): h=aiE+a,E + ...; 4 (8.18) ток i (t) содержит высшие гармоники с частотами nwi, кратными частоте воздействия ©1. Гармоники с частотами 2{0i, 4(0,... обусловлены четными степенями, а гармоники с частотами Зш, Swi, ... - нечетными степенями полинома (8.8). Очевидны также следующие положения: наивысший порядок гармоник совпадает со степенью k полинома, аппроксимирующего характеристику нелинейного элемента; полная фаза л-й гармоники if (t) = nwit -f пв. Выражения (8.15)-(8.18) полностью сохраняют свою структуру при замене постоянной начальной фазы модулированной фазой (t) - 6 imax X X s {t). Из этого следует, что сформулированные выше положения можно распространить также и на воздействие частотно-модулированного сигнала на безынерционный нелинейный элемент (при постоянной амплитуде). Необходимо лишь каждую из гармоник тока с амплитудой /„ трактовать как несущее колебание, модулированное по углу. Это объясняется тем, что при угловой модуляции амплитуда колебания, несмотря на возникновение спектра боковых частот, остается неизменной. Для первой (основной) гармоники индекс угловой модуляции совпадает с Qimax"!. а для ВЫСШИХ гармоник индекс пвхшдх =«"1- Соответственно но в п раз увеличивается и девиация частоты. Сказанное иллюстрируется рис. 8.9. Частота модуляции Q со. С увеличением номера гармоники ширина спектра боковых частот возрастает, но, как отмечалось выше, амплитуда суммарного колебания остается равной /„. 2(У Зы ы 2(У, 5(У/ ы О а) б) Рис. 8.9. Спектр тока при гармоническом воздействии на резистивный элемент (а) и то же при частотной модуляции (б) 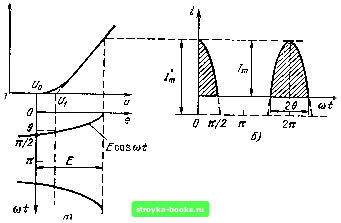 Рис. 8.10. Существенно нелинейный режим работы усилительного прибора Для амплитудно-модулированного колебания, когда Е ~ Е (t), нелинейность характеристики может корентатм образом исказить форму передаваемого сигнала. Этот вопрос рассматривается в § 8.5, 8.7. Рассмотрим теперь работу нелинейного элемента в режиме существенно более нелинейном (рис. 8.10, а), получаемом при сдвиге рабочей точки и о влево и соответствующем увеличении амплитуды возбуждающего напряжения Е. В данном случае целесообразно применить кусочно-линейную аппроксимацию вольт-амперной характеристики (см. § 8.2, комментарий к рис. 8.7, а). При гармоническом возбуждении ток i (t) приобретает импульсную форму (рис. 8.10, б). Угол 6, соответствующий изменению тока от максимального значения до нуля, получил название угла отсечки тока. Длительность импульсов тока равна 26 (см. рис. 8.10, б). Из рис. 8.10, а очевидно следующее выражение: cos е = (t/i - Uo)/E. Амплитуда тока 1т = ailE- (t/i - t/o)l = аЕ (1 - cos 6), (8.19) (8.20) где fli - крутизна линейной части вольт-амперной характеристики [см. (8.9)1. При гармоническом возбуждении нелинейного элемента форма импульса тока в пределах -6 •< со/<; 6 близка к отсеченной косинусоиде и, если пренебречь кривизной вольт-амперной характеристики на нижнем сгибе (см. рис. 8.10, а), мгновенное значение тока можно выразить уравнением г (/)=/;, (cos со/-cos 6), - е<{о/<е. (8.21) Символом Im обозначена амплитуда импульса, которая получилась бы при 6 = л/2. Так как амплитуда реального импульса соответствует моменту (nt = О, имеет место соотношение /m = J(0)=/;(l-COSe), откуда /;г = /т/(1-cosO). 8* 227 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [ 74 ] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] [167] [168] [169] 0.0014 |
|||||||||||||||||||||||||||||||||||||