Как видим, в частном случае и>. = ю,, колебание с нижней комОинаци-онной частотой вырождается в постоянный ток

io=a2£rCOs(e,-9,:) £„. (8.76)

При Og - 6 = О или л ток Ifoi достигает максимума, при G.- 9 = = я/2 ток го = 0.

При включении на выходе преобразователя фильтра нижних частот колебание с частотой 2(0., подавляется и на выходе фильтра остается одно лишь постоянное напряжение, пропорциональное току /о.

При наличии AM, когда е., (t) - Eg (t) cos (coj + 9), колебание на выходе будет пропорционально току:

ia it) =а.2 Е, cos (6, -0) Е, (t), (8.77)

т. е. будет совпадать по форме с законом модуляции аплитуды высокочастотного колебания eg (t).

Иными словами, на выходе преобразователя выделяется передаваемое сообщение, причем по отношению к входному колебанию при Eg (t) < Е обработка по существу является линейной.

Основным преимуществом такого способа обработки, называемого синхронным детектированием, является повышенная избирательность радиоприема слабых сигналов на фоне шума (устраняется взаимодействие сигнала с помехой в нелинейном устройстве, каковым является обычный амплитудный детектор).

Следует, однако, отметить, что реализация принципа синхронного детектирования связана со значительными трудностями, так как обеспечение синхронизма частоты гетеродина с частотой принимаемого сигнала является сложной задачей, особенно при приеме слабых сигналов на фоне помех.

8,13. ПОЛУЧЕНИЕ АМПЛИТУДНО-МОДУЛИРОВАННЫХ КОЛЕБАНИЙ

В § 8.4 указывалось, что при воздействии на нелинейный резистивный элемент с квадратичной характеристикой двух гармонических колебаний с частотами Wj и «2. отвечающими условию < ы., в спектре тока среди других спектральных составляющих можно выделить три частоты coj, tOj + (Oi и (02 - «1, образующие спектр AM колебания.

В генераторах и передатчиках серьезным требованием является получение большой мощности колебания при хорошем КПД. Ясно, что квадратичный режим работы нелинейного элемента этому требованию не отвечает. Для улучшения энергетических показателей модуляции резистивный нелинейный элемент должен работать в существенно нелинейном режиме, с отсечкой тока. Поэтому модуляция амплитуды высокочастотного колебания сводится к воздействию модулирующим напряжением на нелинейный резонансный усилитель. Структурная схема устройства для получения AM колебаний представлена на рис. 8.44.

На вход нелинейного резонансного усилителя, работающего с отсечкой тока, подается несущее колебание с частотой ojq от независимого источника (автогенератора). Модулирующее колебание (сообщение) s (t), спектр которого расположен в области частот, низких по сравнению с Шц, изменяет положение рабочей точки на вольт-амперной характеристике нелинейного элемента и в результате изменяется амплитуда на выходе.

Одна из возможных схем подачи модулирующего колебания s (t) на резонансный (транзисторный) усилитель показана на рис. 8.45. Конденсатор Cg

25,5

Рис. 8.44. Структурная схема устройства для получения AM колебания

Рис. 8.45. Принципиальная схема к рис. 8.44 "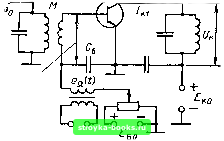

s(t);a

и - I 7

В цепи база - эмиттер защищает низкочастотную цепь от токов высокой частоты.

Режим работы нелинейного усилителя при модуляции поясняется рис. 8.46, а, построенным для тональной AM (s (/) - гармоническая функция с частотой Q).

Так как ток коллектора („ = Ро- то амплитуда напряжения на колебательном контуре, создаваемого первой гармоникой коллекторного тока.

От рассмотренного в § 8.3 рнс. 8.10 отличие заключается в зависимости амплитуды импульсов тока (рис. 8.46, б) от модулирующего напряжения (t). Это приводит к изменению амплитуды первой гармоники коллекторного тока и, следовательно, к из.менению амплитуды напряжения на колебательном контуре усилителя. .Модулированный по а.мплитуде ток основной частоты Ып показан на рис. 8.46. в. Штриховой линией обозначено изменение /„1 - амплитуды первой гармоники тока.

При правильном выборе амплитуды модулирующего напряжения изменение амплитуды импульсов Д/ относительно исходного значения /,„,, связано с еа линейным соотношением

А/™ -=К

ам - постоянный КОЭффИЦИСНТ.

Поэтому огибающая импульсов изменяется по .закону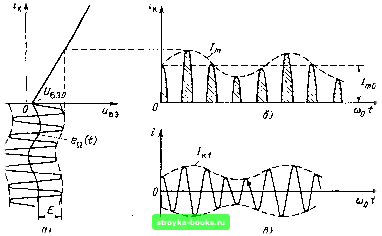

Рис. 8.46. Режим работы нелинейного резонансного усилителя при .М 256

а амплитуда первой гармоники коллекторного тока - по закону

Так как изменение (О во времени (при постоянной амплитуде Е высокочастотного колебания) сопровождается изменением угла отсечки 9 и соответственно коэффициента (9), то форма функции /«1 (t) отличается от формы ва (t). Отсюда видно, что при модуляции смещением неизбежны искажения передаваемого сообщения. Искажения могут быть достаточно малыми при правильном выборе пределов изменения угла отсечки и работе сне слишком глубокой AM (40-50 %).

8.14. РЕЗОНАНС В КОЛЕБАТЕЛЬНОМ КОНТУРЕ С НЕЛИНЕЙНОЙ ЕМКОСТЬЮ

Широкое распространение получили электронные способы управления резонансной частотой колебательной системы с помощью варикапа, подключаемого к основной емкости контура.

Рассмотрим некоторые особенности резонансных явлений в контуре, у которого г и L линейные (и постоянные) элементы, а С = С («с) - нелинейная, зависящая от напряжения емкость. В контур включен источник гармонической ЭДС е (t) = Е cosat; амплитуда Е поддерживается неизменной, а частота ю медленно изменяется, как это обычно делается при снятии резонансной характеристики контура.

Исходим из дифференциального уравнения

Ь - +п + ис=Е cos (ot. (8.78)

Переходя от тока i к заряду q и учитывая, что i = dq/dt, а напряжение на емкости uc = q/C (uc), переписываем уравнение (8.78) в форме

d"" q . г dq . Е -2 ---1. -- --- о = - COS

dt L dt LC(Uc) L

Заметим, что нелинейная емкость С (цс) является функцией и q. Поэтому слагаемое q можно представить в виде нелинейной функции / (q), а дифференциальное уравнение можно записать в виде

+ 2а +/(?)= cos со/, (8.79)

ар dt L

где а = r/2L.

В отсутствие нелинейности функция / (с?) должна обращаться в ,\ q=

= СОо 9, где Со = l/cooL. Поэтому функцию / (q) удобно аппроксимировать выражением

f(.q)=lq+hq\ (8.80)

где 63- параметр, учитывающий нелинейность вольт-кулонной характеристики конденсатора при больших амплитудах.

Выбор такой аппроксимации, значительно упрощающей анализ нелинейного уравнения, не снижает существенно общности выводов (по крайней мере, качественных).

Подставляя (8.80) в (8.79), приходим к уравнению

+ 2а+из*? -