nrv-v-i

e(t)

-O-r-

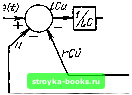Интегратор

Интегратор

Рис. 8.51. Линейный четырехполюсник

Рнс. 8.52. Структурная схема моделирования уравнения (8.109)

уравнения системы результаты аналогового моделирования нетрудно затем преобразовать в алгоритм моделирования на цифровой ЭВМ.

Моделирование дифференциального уравнения проиллюстрируем сначала на примере линейной цепи, показанной на рис. 8.51. Напряжение (в операторной форме) на выходе цепи

\1Ср

Lp4-r+\/Cp /.Cp2-f-rC/)-f 1 Перепишем это выражение в форме Е (р) = LCp и (р) + rCpU (р) -j-U(p).

(8.107)

Учитывая, что умножение U (р) на р эквивалентно дифференцированию и (t), а умножение на р эквивалентно двухкратному дифференцированию, приходим к следующему дифференциальному уравнению:

e{t)LC

d + rC + uit)LCu + rCu-u.

dt dt

(8.108)

Решим это уравнение относительно наивысшей производной: ЬСи - е - гСи-

(8.109)

Уравнению (8.109) соответствует схема на рис. 8.52. Основными эле" ментами этой схемы являются интеграторы на операционных усилителях, сумматоры и умножители на число. Выходы интеграторов ими характеризуют состояние системы в рассматриваемый момент времени / с учетом начальных условий, т. е. состояния в момент времени о. а также с учетом действия входного сигнала на интервале от /„ до t. В этом смысле выходы интеграторов и и и называют переменными состояния, а основанный на них способ интегрирования дифференциальных уравнений называют методом переменных состояв и я (МПС).

По существу, представленное на рис. 8.52 устройство, основанное на применении интеграторов, решает заданное дифференциальное уравнение (8.108) и определяет реакцию цепи (см. рис. 8.51) на воздействие е (t).

Принцип построения схемы, описанный выше, можно применить и для моделирования нелинейной системы. В качестве иллюстрации построим

1 Этот метод получил особенно широкое распространение при анализе линейных систем со многими входами и выходами, когда эффективно применение матричного исчисления и векторного анализа для операций с большим числом переменных, входящих в исследуемые задачи [8].

В данном случае нас будет интересовать применение МПС к нелинейным задачам. (См. Деруссо П., Рой Р., Клоуз Ч. Пространство состояний в теории управления: Пер. с англ. - М.: Наука, 1970.

схему, соответствующую нелинейному дифференциальному уравнению (8.81), которое запишем в форме

(7 = - cos u>t --2aq~u)b q + bgq-.

(8.110)

Схема представлена на рис. 8.53. Дополнительно к двум интеграторам и сумматору потребовался функциональный блок, осуществляющий операцию возведения в куб функции q (t).

Определение реакции нелинейных цепей на заданное воздействие решением дифференциального уравнения требует, как правило, больших вычислительных затрат. Задача упрощается, если рассматриваемая нелинейная система допускает дискретное представление процессов, происходящих в отдельных ее элементах, как линейных, так и нелинейных. Такое положение имеет место, в частности, если нелинейные элементы являются безынерционными. В подобных случаях открывается путь к эффективному цифровому моделированию.

Покажем это на примере моделирования простого амплитудного детектора (см. рис. 8.24). Вольт-амперную характеристику диода представим в виде нелинейной функции

д=/("д) = /(-"вых).

(8.111)

где "д = е - - напряжение, действующее на диоде.

Соотношение между токами в линейной части схемы определяется выражениями

1«(0 + с(0=гд(0. hit)-

откуда вытекает следующее нелинейное уравнение:

~ + "вых it)=f\e it) - «еых (01

Ul д

С"яых=/(е-"ьых) -

(8.112)

Это уравнение моделируется аналоговой структурной схемой, представленной на рис. 8.54. На выходе сумматора 1 образуется разность е - «вых> которая после нелинейного преобразования в диоде дает ток /д, т. е. первое слагаемое в правой части (8.112).

Нелинейное безынерционное преобразование (8.111) легко реализуется в ЭВМ. Функция / (Ujj) может быть задана либо в виде таблицы (например, по экспериментальным данным), либо аналитически. В первом случае таблица должна храниться в памяти ЭВМ, во втором случае вычисление значений

1д производится по программе, соответствующей аналитическому выражению.

Переходя к дискретному моделированию, задаем шаг Т исходя из наивысшей частоты в спектре входного сигнала е (t), руководствуясь правилами, изложенными в § 2.17.

Таким образом, входящие в уравнение (8.112) величины е (t).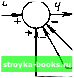

Рис. 8.53. Структурная схема моделирования уравнения (8.112)

"вых (О и 1д (О ДОЛЖНЫ быть заме-нены соответственно, на е (тТ), / - "вых (тТ) и (д (тГ).

Для перехода от дифференци-

ального уравнения (8.112) к эквивалентному ему разностному уравнению воспользуемся соответствием

dusuxit) «вых («Л-«вых ("Т -л

Интеаратор

(8.113)

Рис. 8.54. Структурная схема моделирования уравнения (8.112)

которое имеет смысл при условии достаточной малости Т. Тогда уравнение (8.112) принимает вид

-r ["вых (тТ)-иАтТ-Т)\ = /[е(тТ)-ив,(тТ)\-

--г- «вых imT)

"вых("1Т) =

Rf\e{tnT)~UB,{tnT)] +

вых(тГ-7),

(8.114)

Z+T

где т = RC\ а„ = Т/ (х + Т); = х/ (х + Т).

Уравнению (8.114) соответствует схема, представленная на рис. 8.55, а, а общая аналоговая схема (см. рис. 8.54) после перехода к дискретной обработке принимает вид, показанный на рис. 8.55, б.

Из сопоставления аналоговой и дискретной схем следует,что звено с задержкой Т в кольце обратной связи для разностного уравнения аналогично интегратору для дифференциального уравнения. Характеристики и свойства подобных устройств обсуждаются в § 12.8.

Моделирование рассматриваемой цепи целесообразно в тех случаях, когда аналитическое решение затруднительно или даже невозможно. Подобная ситуация имеет место, например, при детектировании относительно коротких радиоимпульсов, когда в пределах длительности импульса укладывается всего лишь несколько периодов высокочастотного заполнения и условие (8.56) оказывается невыполнимым (см. § 8.9).

Пусть, например, средняя частота заполнения /о - 1/Го = 465 кГц (Промежуточная частота в обычно.м радиоприемнике), а длительность им-

е(тТ)-иьь\-(тТ)

иъыхСгпР)

Рис. 8.55. Дискретный вариант схемы, представленной на рис. 8.54

1 Постоянная времени т= i?C, как правило, значительно больше периода высокочастотного заполнения входного сигнала е (i), так что спектр выходного напряжения «вых (О много же спектра сигнала е (t). Следовательно, при значении Г, обеспечивающем сохранение информации, которая содержится как в е (t), так и в / [е (t)], наверняка выполняется (8.113).