в соответствии с условием (9.49) изоклины С и D отсутствуют. Каркас фазового портрета определяется только прямой А и условием пересечения оси X под прямыми углами. При а/юд > О угловой коэффициент этой прямой в соответствии с уравнением (9.50) отрицателен. Соответствующий этому случаю фазовый портрет, представляющий собой скручивающуюся к началу координат спираль, изображен на рис. 9.21. Из любого начального положения изображающая точка с течением времени приближается к началу координат, являющемуся точкой устойчивого равновесия. Эта точка называется особой точкой типа устойчивого фокуса.

Рассмотрим случай -1 < а/шо<; О (колебательная система с инкрементом). Фазовый портрет отличается от показанного на рис. 9.21 лишь тем, что спираль раскручивается и изображающая точка удаляется от начала координат. Точка х = О, у - О является особой точкой типа неустойчи-вогофокуса.

Применительно к рассматриваемому в следующем параграфе фазовому портрету автогенератора особый интерес приобретает случай а = 0. когда уравнение (9.45) вырождается в уравнение гармонического колебания

х + ш1х = 0,

решение которого, как известно, имеет вид

х = Q sin ((Оц t + ф), y - x-iHoQ cos (ш t + ф).

Здесь Q - амплитуда заряда конденсатора контура. Уравнение фазовой траектории (9.47) при а = О

(9.51)

(9.52)

dx у

- уравнение с разделяющимися переменными, которое легко интегрируется:

ydy-\-(olxdx=0, i/* + u)§A:2 = cosnt = C. (9.53)

Подставляя вместо хи у выражения (9.52), получаем со§ cos2 (сОо / + ф) + sjn2 / -)- ф) = cog С.

Разделив обе части уравнения (9.54) на С, придем к выражению

yVcogQ + xVQl, (9.54)

представляющему собой уравнение эллипса с горизонтальной полуосью Q и вертикальной полуосью coqQ (рис. 9.22).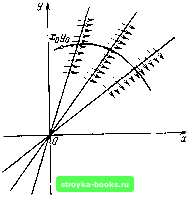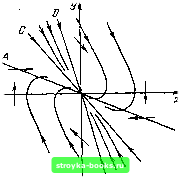

Рис. 9.19. К построению фазового портрета по методу изоклин

Рис. 9.20. Фазовый портрет апериодиче ской системы при а/й)о> 1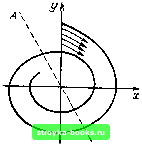

Рис. 9.21. Фазовый портрет системы затуханием при 0<а/(Оо<1

Рис. 9.22. Фазовый портрет системы, описываемой уравнением (9.54) при а = 0

Итак, при а = О фазовые траектории представляют собой семейство эллипсов с общим центром в начале координат, причем размеры осей эллипса определяются амплитудой гармонического колебания, т. е. в конечном счете энергией, запасенной в системе. Эта энергия может быть выражена в виде 0,bCQ (максимальная энергия в емкости) или в виде (L/2) (coqQ) (в индуктивности). Так как потери отсутствуют, то запас энергии остается неизменным («консервативная» система) и каждому значению запаса энергии соответствует свой эллипс.

9.8. ФАЗОВЫЕ ПОРТРЕТЫ АВТОГЕНЕРАТОРА

Итак, гармоническому движению системы соответствует замкнутая фазовая траектория на фазовой плоскости (эллипс). В более общем случае сложного периодического движения (не обязательно гармонического) фазовая траектория может иметь сложную форму, но она обязательно является замкнутой.

Автоколебательной системе с устойчивым стационарным состоянием на фазовой плоскости соответствует замкнутая кривая, к которой приближаются соседние фазовые траектории. Для выявления формы этой замкнутой интегральной кривой, а также характера этого приближения рассмотрим на фазовой плоскости всю картину установления автоколебаний, от запуска генератора до установления стационарного состояния.

В начале процесса система является линейной и описывается уравнением (9.8), совпадающим с уравнением (9.45). Для удобства вместо (9.9) будем исходить из уравнения

-е

du dx

-f u = О,

(9.55)

получающегося из нелинейного уравнения (9.38) при замене «ак на ы и пренебрежении величиной по сравнению с единицей. Напомним, что в этом уравнении е = 2оэк/шо. а т = Wgt.

Так как при выполнении условия самовозбуждения е положк-"ельно [см. (9.36)1, соответствующая начальному этапу фазовая траектория имеет вид раскручивающейся логарифмической спирали (особая точка типа неустойчивого фокуса).

Когда с ростом амплитуды колебаний начинает проявляться нелинейность системы, увеличение радиуса спирали замедляется и в пределе (теоретически при / оо) фазовая траектория превращается в окружность с радиусом t/cr. равным стационарной амплитуде колебания.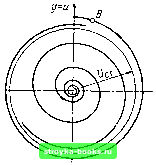

Рис. 9.23. Фазовый портрет ан-токолебания при мягком режиме возбуждения

Если начальное положение изображающей точки задать вне ок1>ужностн радиуса (/ (точка В на рис. 9.23), то движение изображающей точки будет происходить по скручивающейся спирали (так как при U > е отрицательно) до перехода на окружность радиуса U..

В силу устойчивости стационарного состояния автогенератора (в данном случае с мягким самовозбуждением) при любых начальных условиях изображающая точка переходит на окружность радиуса бд.,.

Изолированная замкнутая кривая на фазовой плоскости, к которой с возрастанием / приближаются (по спирали) с внутренней и внешней стороны соседние фазовые траектории, называется предельным циклом. Устойчивость предельного цикла носит название орбитной или орбитальной устойчивости.

Легко представить себе, что в случае автогенератора с жестким режимом самовозбуждения к предельному циклу будут стягиваться только фазовые траектории, радиус которых больше некоторого критического зна>*ения, соответствующего амплитуде в точке D на рис. 9. И. Если начальные условия запуска автогенератора таковы, что начальная амплитуда меньше этого значения t/n,in, то изображающая точка на фазовой плоскости будет двигаться по скручивающейся спирали, постепенно приближаясь к началу координат, являющемуся в данном случае точкой устойчивого фокуса (рис. 9.24).

Допустим, что после установления стационарного режима в колебательный контур автогенератора каким-либо образом была введена дополнитель-най энергия, в результате чего амплитуда и фаза колебания получили мгновенные приращения: первая на величину AU, а вторая на угол фо. Отклонение изображающей точки от предельного цикла, соответствующее этому возмущению, выразится в переходе на спираль с радиусом i/p.f -f /S.U и в изменение фазы колебания на сро (рис. 9.25).

Через некоторое время изображающая точка перейдет по скручивающейся спирали (штриховая линия на рис. 9.25) на предельный цикл, соответствующий стационарной амплитуде. Фазовый же сдвиг фо не компенсируется, так как в автогенераторе отсутствуют факторы, которые фиксировали бы начальную фазу колебания.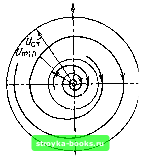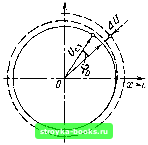

Рис. 9.24. Фазовый портрет автоколебания при жестком режиме возбуждения

Рис. 9.25. К вопросу об орбитальной устойчивости предельного цикла