в заключение отметим, что предельный цикл имеет форму круга при строго гармонической форме генерируемых колебаний. В действительности эта форма искажается наложением высших гармоник. В автогенераторах, близких к консервативным (с высокодобротной колебательной системой), влиянием гармоник можно пренебречь. В случае же генераторов релаксационного типа предельный цикл может иметь весьма сложную форму (например, близкую к прямоугольной).

Как отмечалось в предыдущем параграфе, для нелинейных систем фазовые траектории строятся с помощью графоаналитических методов (например, метода изоклин).

9.9. АВТОГЕНЕРАТОРЫ С ВНУТРЕННЕЙ ОБРАТНОЙ СВЯЗЬЮ

При рассмотрении механизма возникновения колебаний в автогенераторе (см. § 9.2) мы встретились с понятием отрицательного сопротивления, вносимого в колебательный контур при надлежащем выборе фазы обратной связи. При этом в соответствии с обобщенной схемой автоколебательной системы (см. рис. 9.1) имелась в виду внешняя обратная связь.

Существуют, однако, некоторые электронные приборы, которые позволяют получить отрицательное сопротивление за счет падающих участков вольт-амперной характеристики без введения в схему специальных элементов обратной связи. К таким приборам относятся, например, туннельный диод и обычные тетроды и пентоды при соответствующем подборе напряжений на электродах.

На рис. 9.26 показана вольт-амперная характеристика туннельного диода, представляющая зависимость прямого тока диода от положительного напряжения смещения. На падающем участке а-б дифференциальное сопротивление диода отрицательно:

R =du/di„=ctgY,

где у - угол наклона касательной к кривой (д = / (и) в рабочей точке Uq.

При подключении электронного прибора с подобной вольт-амперной характеристикой к колебательной цепи можно осуществить генерацию высокочастотных колебаний. При этом получается автогенератор с внутренней обратной связью.

На рис. 9.27 изображена схема генератора на туннельном диоде. В качестве емкости контура в генераторах СВЧ обычно используется собственная емкость диода €„. Блокировочные дроссель Lg;, и конденсатор Cg,,, (Сдл > Со) защищают цепь постоянного тока от тока высокой частоты; г„ - сопротивление потерь в кристалле и в элементах контура.

Схема замещения контура, шунтированного отрицательным сопротивлением R-, изображена на рис. 9.28. По отношению к этому сопротивлению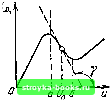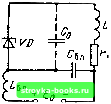

Рис. 9.26. Вольт-ампер-иая характеристика туннельного диода

Рис. 9.27. Автогенератор на туннельном диоде

Рис. 9.28. Схема замещения автогенератора на туннельном диоде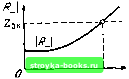

Рис. 9.29. К определению стационар-нон амплитуды автоколебания в генераторе с внутренней обратной связью

напряжение и„, действующее на колебательном контуре, рассматривается как ЭДС, так что ток через диод (д = -ujR-.

Колебательное напряжение на контуре и токи il, ic, гд связаны между собой соотношениями

" u, = rJi. + L. (9.56)

(пс, 1с

В качестве искомой функции выберем, например, ток (/, в индуктивной ветви контура. Исключая из первого уравнения (9.56) ic i}) с помощью второго и третьего уравнений, получаем

d iL dt

+ LC-

d4 dt

Однако

Jl + L

dij \ ~1Г

Приравнивая правые части приведенных выражений, после группировки слагаемых получаем следующее дифференциальное уравнение:

iL = 0.

Для того чтобы амплитуда колебаний нарастала, коэффициент при первой производной должен быть отрицательным. Отсюда получается условие возникновения колебаний

JjL L

<0

\R-\<

= 2з„р==р(3 =

(Ор с

(9.57)

где Р - абсолютная величина отрицательного сопротивления; р - эквивалентное резонансное сопротивление контура; Q-добротность; р = = У L/C - характеристическое сопротивление контура.

Когда сопротивление \R-\, зависящее от амплитуды колебания (при переходе на нелинейную часть характеристики), увеличится до

i/? (t/J=Z3„p,

в автогенераторе установится стационарная амплитуда колебаний. Режим устойчив, если в точке пересечения горизонтали 2э„ р кривая \R {Uk)\ имеет положительный наклон (рис. 9.29). Все, что в предыдущих параграфах было сказано о характере нелинейной зависимости средней крутизны от амплитуды управляющего напряжения, в данном случае можно распространить на характер зависимости величины, обратной \R-\, от напряжения f/„ .

Преимуществом туннельного диода является весьма малое по абсолютной величине отрицательное сопротивление (~ 10-100 Ом). Несмотря на относительно большую собственную емкость диода (несколько десятков пикофарад), условие самовозбуждения (9.57) выполняется в весьма широком диапазоне частот, вплоть до СВЧ, Так, при добротности контура Q - 50, собственной емкости диода С„ = 50 пФ и /? = 50 Ом предельная частота генера1ши Q 2л \R\C„ % 3 10» Гц 3000 МГц.

9.10. АВТОГЕНЕРАТОР С ЛИНИЕЙ ЗАДЕРЖКИ В ЦЕПИ ОБРАТНОЙ СВЯЗИ

Пусть имеется автогенератор с избирательной нагрузкой и линией задержки в кольце обратной связи. Подобный генератор можно представить в виде обобщенной схемы (рис. 9.30), аналогичной схеме на рис. 9.1. Рассматривая линию задержки как идеальныйчетырехполюсник с передаточной функцией е"", можно представить линейную часть схе.мы. состоящую из колебательного контура и линии задежки Т. в виде одного четырехполюсника обратной связи с передаточной функцией f

К„,(«о -О) ) Л:„(о» o)j,)e<e

где К,: - модуль передаточной функции колебательного контура с резонансной частотой со,,: с(,,. - ФХЧ контура. В гюлосе прозрачности контура можно считать, что (( х - (о) - ю,,) т„, где т,, - постоянная времени контура.

Введение в схему линии задержки не изменяет модуля передаточной функции, но существенно влияет на результирующую ФЧХ

q V -((О - (Ор) т. - юГ.

При достаточно большой задержке Т наклон результирующей ФЧХ определяется в основном слагаемым со Г, причем может оказаться, что в полосе прозрачности колебательной цепи изменение достигает большого значения, превышающего несколько полных оборотов 2л. Подобный случай изображен на рис. 9.31, на котором со 2, со..,, со,, cOj, ... - частоты, лежащие в полосе прозрачности контура, при которых ординаты ФЧХ (р равны п2л, где п - целое число. Так как при указанных частотах выполняется баланс фаз и амплитуд (см. § 9.3), каждая из них может являться частотой автогенерации. Введение в кольцо обратной связи достаточно большой задержки придает системе многочастотный характер. Роль колебательного контура при этом сводится лишь к ограничению числа частот, на которых обеспечивается усиление, необходимое для автогенерации.

Возникает вопрос, могут ли одновременно устойчиво существовать несколько автоколебаний с различными частотами. Это зависит от таких факто-

Г"

Нелинейный элемент

Колебательная цепь

Линия задержки Т

Рис. 9.30. Автогенератор с линией задержки в цепи обратной связи