Дится к уменьшению сопротивления потерь в контуре на величину отрицательного сопротивления

(9.62)

Таким образом, эквивалентное активное сопротивление регенерированного контура

а д обротность

Гэк (r - MS!C)

Отношение

Q3k/Qo= 1

MS/C

где Qo = p/ - добротность нерегенерированного контура, можно рассматривать как усиление схемы на резонансной частоте со = Шр, когда coL - - 1/соС = 0.

Увеличением М можно добиться существенного увеличения (?эк и, следовательно, повышения усиления. Следует, однако, иметь в виду, что увеличение при заданной и неизменной резонансной частоте контура сор приводит к сужению полосы пропускания контура. Кроме того, возникает проблема устойчивости цепи. При

MS Ст

(9.61)

цепь теряет устойчивость, а при MSiCr> 1 возникают автоколебания, т. е. усилитель превращается в генератор.

Иначе обстоит дело при больших амплитудах напряжения на входе усилителя. Увеличение амплитуды на зажимах база - эмиттер приводит к уменьшению средней крутизны S и в соответствии с (9.62) к уменьшению rjp. Зависимость Sp и гр от амплитуды приводит к нелинейным искажениям усиливаемого сигнала.

Подставляя Sep вместо S в выражение (9.61), получаем

1 § Ё

г-MScp/C-fi (wL -1/шС) эк + (mZ, -l/wC)

а при резонансе

/тах-£/Гэ„, (9.61")

где Гэ„-г-уИ5ер/С. (9.63)

Из выражения (9.6Г) следует, что при усилении AM сигнала, когда Е = Е (t), амплитуда тока / (/) будет изменяться по закону, отличному от закона модуляции Е (t) (из-за зависимости Sep от амплитуды колебания). Возникает нелинейное искажение усиливаемого сигнала, сопровождающееся образованием новых частот.

Нелинейный характер рассматриваемой цепи (при больших амплитудах Е) влияет также и на форму резонансной характеристики регенерирован-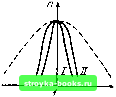

0)/б)р

Рис. 9.40. Резонансные характеристики регенерагивпого контура:

/ - при малых; - при больших амплитудах: штриховая линия - в отсутствие регенерации

ного контура. Действительно, при отклонении частоты входного сигнала (О от резонансной частоты сор возрастает реактивное сопротивление х = coL- - 1/(иС в (9.61), что приводит к уменьшению амплитуды тока /. Но уменьшение / в свою очередь приводит к уменьшению и г из-за возрастания S [см. (9.63)[, что в некоторой степени компенсирует влияние возрастания х. В результате резонансная характеристика в верхней части уплощается, и тем сильнее, чем больше амплитуда внешней ЭДС, действующей на контур. При значительных расстройках преобладающее влияние на амплитуду оказывает реактивное сопротивление и резонансная характеристика быстро спадает почти до нуля (рис. 9.40).

Из всего сказанного следует, что регенерацию можно эффективно использовать только для усиления слабых сигналов.

С явлением регенерации часто приходится встречаться в радиотехнике. Иногда регенерация возникает в усилительных устройствах из-за наличия паразитных обратных связей, что может приводить к искажению сигналов.

9.13. ДЕЙСТВИЕ ГАРМОНИЧЕСКОЙ ЭДС

НА АВТОГЕНЕРАТОР. ЗАХВАТЫВАНИЕ ЧАСТОТЫ

Поведение автогенератора, находящегося под действием виепшей силы, существенно зависит от амплитуды и частоты этой силы.

Если амплитуда возбуждения очень мала по сравнению с амплитудой автоколебания и одновременно частота м значительно отличается от частоты О), = (Ор свободного автогенератора (Юр - резонансная частота контура автогенератора), то действие внешней ЭДС сводится к эффекту модуляции, который проявляется в изменении фазы и амплитуды автоколебания по весьма сложному закону. С приближением частоты оо к оор картина меняется. Частота генерации (о,, «подтягивается» к частоте оо внешней ЭДС, и при некотором значении До) (о - сор; зависящем от соотношения амплитуд, автогенератор начинает работать точно на частоте со,, --- со без каких-либо признаков .модуляции. Частота генератора оказывается «захваченной» частотой вынуждающей силы.

Явление захватывания частоты используется в ряде радиотехнических устройств, когда требуется осуществить принудительную синхронизацию автогенератора с помощью маломощного источника колебаний. В некоторых случаях, например при наличии паразитных связей между двумя автогенераторами, захватывание возникает произвольно и препятствует независимой их работе на близких частотах.

Рассмотрим механизм явления захватывания частоты в простейшем од-ноконтурно.м автогенераторе с транс(юрматорной обратной связью при последовательном включении внешнего источника ЭДС в цепь база - эмиттер (рис. 9.41). Следует подчеркнуть, что такая схема выбрана только для определенности рассуждений. С точки зрения установления общих соотноше-•ний вид схемы автогенератора и способ введения вынуждающей ЭДС принципиального значения не имеют. Частоту генерации (в отсутствие внешней ЭДС) приравняем резонансной частоте контура сор = IiVlC.

Рассмотрим сначала баланс фаз в автогенераторе, находящемся под действием внешней ЭДС е (t) = Е cos («/-f 9ц), в предположении, что имеет место стационарный режим захватывания, т. е. генерируемая частота равна частоте со, отличной от резонансной частоты контура ODp. При этом амплитуду Е будем считать настолько малой, что все основные параметры автоколебания - амплитуда первой гармоники коллекторного тока амплитуда напряжения на контуре (У,, и амплитуда напряжения обратной связи (Урр - останутся такими же, как и в отсутствие внешнего воздействия.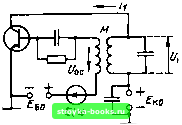

Рис. 9.41. .Литогенератор с синхронизи рующим источником ЭДС в цепи база- эмиттер

Рис. 9.42. Векторные .1маграммы нанря

жений и тока в автогенераторе:

и) бе; BHtnuHii-n ноздействия; о) н \нжнц,-

.чахнятывання частоты

Иными словами, влияние BHeujHcro воздействия проявляется то.1Ько в изменении фазовых соотно1нений в автогенераторе.

До включения источника внеигней ЭДС эти соотнонгения характеризуются векторной диаграммой, показанной на рис. 9.42, а. Ток 1, - в фазе с напряжением Uo., U,,., а напряжение U,,. в фазе с током 1, (напряжение на контуре отсчитывается от эмиттера к коллектору).

Исходная фаза тока 1, выбрана произвольно, так как в автогенераторе фаза автоколебания зависит от начальных условий запуска. После включения внешней ЭДС е (i) =--- Е cos at (начальная фаза 8,, приравнена нулю) и установления стационарного режима диаграмма примет вид, показанный на рис. 9.42, б. При построении этой диаграммы учтены следующие условия:

а) между током I, и напряжением имеется фазовый сдвиг q,,, зависящий от расстройки контура по отношению к генерируемой частоте to. Принимая для определенности, что о) <с о)р, приходим к выводу, что вектор и,, должен опережать вектор I, на угол

((,= arctg

(9.64)

где Q - добротность контура;

б) ток Ij находится в фазе с результирующим напряжением Uc:

в) напряжение обратной связи М, связанное с напряжением контура и„ соотношением = MML, не .зависит от частоты. Поэтому направления векторов и и,, совпадают.

Из диаграммы видно, что нарушение фазового баланса автогенератора в коллекторной цепи на угол (в сторону опережения) из-за расстройки колебательного контура (при о) < о)р) компенсируется тем, что в цепи база - эмиттер результирующее напряжение Uq,, сдвинуто на угол ф, в сторону отставания относительно Uqc-

Когда о) > ojp, фазовый сдвиг в коллекторной цепи является запазды вающим, а в цепи база - эмиттер - опережающим.

Из условий б) и в), а также непосредственно из диагра.ммы на рис. 9.42, б вытекает следующее равенство:

sintj-v - £sinф„, ty,-„, где (),,. - фазовый сдвиг между Е и Uj,.

(9.65)

Эту диаграмму удобно строить исходя из произвольно выбранного положения вектора 1,, после чего вся диаграмма должна быть повернута на угол, при котором положение вектора Е соответствует заданной начальной фазе 6п внешней ЭДС.