
 |
|
Главная Интегральные схемы [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [ 25 ] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] сопротивление, тем больше ток при заданном напряжении. Электрическая цепь или некоторый ее компонент имеет сопротивление 1 Ом, если при приложенном напряжении 1 В в ней течет ток 1 А. По существу это можно выразить в виде одной из трех форм закона Ома: Е == IR, R = E/I, или / = E/R. Здесь Е - напряжение в вольтах, / - ток в амперах и - сопротивление в омах. Обратите внимание, что мы обычно будем иметь дело с токами зна- Рис. 3.12. Простая схема из соединенных параллельно резисторов. Для двух резисторов общее сопротивление определяется формулой R = RiRiKRi + R2). чительно меньше 1 А, которые измеряются в миллиамперах (0,001 А) или микроамперах (0,000001 А), однако эти выражения всегда справедливы, если единицы выбраны правильно. Чтобы облегчить построение электронных схем, существуют специальные компоненты, называемые резисторами, каждый из которых имеет определенное сопротивление, например 1 Ом, 10 Ом, 1 кОм или 1 МОм. На рнс. 3.12 показаны два резистора с сопротивлением по 100 Ом каждый. Если щупы мультиметра, установленного в режим измерения сопротивлений, noaKJiro4atb к каждому из резисторов по отдельности (разумеется, предварительно настроив его на нуль), Рис. 3.13. Параллельное соединение трех резисторов. Для нескольких параллельных резисторов общее сопротивление определяется формулой R = OIRi + MRi + l/Ri + ... + В данном случае R = (1 ?, + 1 ?2 + lRз)-  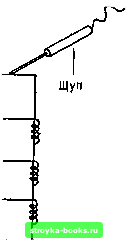 Рис. 3.14.. Измерение сопротивления параллельных резисторов, то он покажет сопротивление 100 Ом. Но если два резистора соединены параллельно, как показано на рис. 3.12, то общее сопротивление окажется меньше, чем сопротивление каждого резистора, в данном случае оно составит 50 Ом. Дело в том, что каждый из резисторов оказывает одинаковое сопротивление протекающему току, и поэтому ток разделится между ними. Основная формула, определяющая полное сопротивление двух резисторов, соединенных параллельно, выглядит так: R = RiR2/{Ri + R2), где и R2 - сопротивления резисторов в омах. Следует запомнить, что при измерении сопротивления в схеме и подключении щупов к резистору, сопротивление которого предположительно составляет 100 Ом, в схеме могут оказаться другие компоненты, подключенные параллельно этому резистору, и в результате измеренное сопротивление будет меньше ожидаемого. В некоторых случаях необходимо бывает отключить один вывод резистора или другого схемного компонента от схемы, а уже затем измерять величину его сопротивления. Иногда может понадобиться измерить полное сопротивление в некоторой точке схемы. На рис. 3.13 показаны три резистора, соединенные параллельно. Их общее сопротивление можно вычислить по формуле R= ll{llRi +IIR2+yRz), где Rl, i?2 и i?3 - сопротивления этих трех резисторов. Эта же формула справедлива для двух резисторов (если отбросить R3), а также для любого числа резисторов, соединенных параллельно (надо добавить в знаменатель IjR, IjRs, l/Re и т. д.). На рис. 3.14 показано, как надо подключать щупы мультиметра при измерении сопротивления схемы, со- -1 I-j R2 1-1 R5 (-\ R4 \ Рис, 3.15. Последовательное соединение резисторов R = Ri-f !+ /?2 -Ь /?з -Ь Ri. Эту цепочку резисторов можно продолжать дальше, [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [ 25 ] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] 0.0009 |
||||||||||