№. It/a

г-изображение оптимального управляющего воздействия на объект регулирования М (г)

h== - BCp(G + F)~lB{C + D) +

+ 2CDVBcosU] GF\

be = BCDGF; Я=Ка -b"/4;

В=.е-

C=e~h De-"; Ge; Fef

s8(s2 + 6s + a)(s + + c)(s + d)(s + g)

при 4a - b>Q

/Co(l+fe,2-i + V 4- bz~* -u

где Ко

acdg

аЛ2(1 2l/~ficosM+ + fi)(l -C)(l-D)(l-G)

bj = - (1 + 2 Kb cos M+C+D+G); 62 = B + C£> + G + 2KB(C + D) X X cosU + (2"KBcosXft + C + D) x X (1 + C);

feg = - В (C + D) - 2CD Kb cos ЯА-- [В + 2 Kb (C + D) cos Яй + CO]x X (1 + G) - (2 Kb cos ЯА + C+D) G;

bi = BCD + [B(C + D) + 2COKb X XcosU] (1 +G)+IB + 2KB(C + + cos ЯЙ +CD] G; 65 = -BCD(l + G)-[B(C + D) + + 2CD Kb cos ЯА]С;

bo = BCDG; X = Ya~ ЬУ4: B=e С = е-; D = е-"; G = e"

58(s2 + bs + a)(s + + c)(s + d)

при 4a -Ь2>0

/Со (1 + + M"+ +

где Ко

ah» (1-~2V В cos %h+ + BH1-C){1-D)

6= (2+2КВсо8ЯА + С + 0); 62=1+B + 2C + 2D + CD + + 2KB(2 + C + D)cos ЯА; 6, = - (1 + B) (C + D) - 2B-2CD- -12KB(1+2C + 2D+CD) cos ЯА;

= В + CD + BCD + 2 ВС + 2BD+ + 2Kb (C + D + CD) cos ЯА;

В табл. 1.2 приведены 2-изображения оптимальных управляющих воздействий

М (2) = 5] «2 (vft+) 2- = 5] mz-

V=0 V»»0 г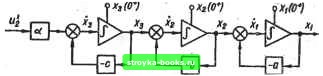

Рис. 1.11

на линейные объекты регулирования в системах (рис. 1.1, а) при единичном ступенчатом воздействии на входе систем и нулевых начальных условиях.

Поскольку в процессе определения оптимальных управляющих воздействий находятся все переменные состоявия объекта, то по выходным переменным (vA*) можно найти входную последовательность «г (vft*) для цифрового регулятора и определить передаточную функцию W (г) цифрового регулятора.

Рассмотрим объект регулирования, математическая модель которого описывается передаточной функцией вида О (s) ==

= а I(s + а) (s + b) (s + c)l~i. Схема аналогового моделирования для объекта регулирования изображена на рис. 1.11, а. Этсгг объект имеет астатизм нулевого порядка. Записывая уравнения динамики объекта регулирования в векторно-матрнчной форме -о = Av, где

Г -а 1 ( Д = 0-610

, • О О -с а

-ООО

определяем расширенную дискретную матрицу перехода для объекта регулирования

А N М aL О В W аР О О С «<? L0 О О I .

где f

Ф(Л) =

bhcB-bC)

(1.42)

A В С

-(b - a)(c - a) + (a - b)(c - b) + (a - c){b - c)

bcA acB abC

{b - «)(c -a)~ (a - b)(c - b)~ {a - c){b - c).

Обозначим u\ (vA+) «= m., н последовательно найдем

г>(0+)=[0: 0; 0; «о]: г» (й+) = \a,Ltno\ аРшо", aQnto; mj;

"af i«Jo 4- «Z,mi

V (2A*)

г> (ЗЛ+) =

где FiAL + PN + QM; F = BP + QW; + MCQ; Sg = 8 + WCQ.

аРШо 4- w/wi aQCm 4- osQmi ma

aSjiTJo 4- аРхЩ + aLmg aSig 4~ aPgrni 4~ 9<2 (C«mo 4- Cmi 4- mj)

= f,+iVFg4-

Чтобы переходные процессы в объекте регулирования при нулевых начальных условиях заканчивались за время, равное 3ft, необходимо равенство вектора г» (3ft+) вектору (при U = I)

1; а; аЬ;

abc а