Передаточная функция W {г) цифрового регулятора

2 «,(vftT«~ ЦитрсШ

•v=0

(i.2)

tluippoScu регулятор

Чшсатор СШып

H(s)

u(t)

e(i)

Цифровой рееувтер

Фиусвтор одъект

Рис. 1.1

Для получения максимального быстродействия при входном воздействии типа ступенчатой функвди и нулевых начальных условиях необходимо, чтобы при О Nh, где N - порядок дифференциального уравнения объекта регулирования; h - шаг квантования мгновенного ключа, ошибка системы равнялась нулю, и входные сигналы интеграторов схемы системы в перемен-

ных состояния также были равны пулю. Используя метод переменного коэффициента усиления, можно для различных передаточных функций G (s) линейных объектов регулирования получить аналитические выражения для коэффициентов передаточной функции W (z) цифрового регулятора (рис. 1.1, а) [19; 23]. Передаточные функции W (г) цифровых регуляторов, обеспечивающих при входном воздействии типа ступенчатой функции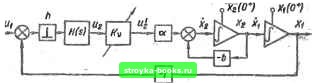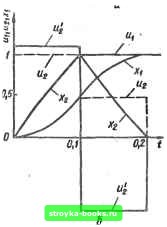

Рис. 1.2

и нулевых начальных условиях оптимальный переходной процесс, различные в зависимости от того, имеет объект регулирования интегрирующие звенья или нет.

Определим передаточную функцию W (г) оптимального цифрового регулятора для системы, имеющей объект регулирования с передаточной функцией G (s)-- а [5 (s-j-fe)]". Объект регулирования имеет астатизм 1-го порядка. Схема аналогового моделирования для такого объекта изображена на рис. 1.2, «. Дрффе-ренциальные уравнения состояния (без учета переменного коэф-фициентя усиления /С) имеют вид =0; = х; *2 = - bxg-

- auji «2 = 0; уравнения переходных состояний: «j (vft+) = Uiivh); Д"! (\h+) = Xi (vft); (vft+) = x (\h); (vft+) = Ui (vft) - Xi (vft). Переписывая уравнения в векторiio-матричной форме v = Av н V (\h = Bv (vft), находим

с учетом усилителя, с переменным коэффициентом усиления определим дискретную матрицу перехода по матрице А в виде:

100 о о 1 Q aPKv 00 В aQKv ООО 1

; Q = y (1-В); Р=(6Л-1+В). (1.3)

Далее на основании соогношення (1.1) последовательно вы-числяем

г>-(0+) = (В»{0)) = [1; 0; 0: 1];

(й) = (Ф (й. Ко) V (0+)) = [1: аРКо-, o.QK„; 1];

ф-(й+) = (Bv(h)f = 11; аРКо. aQKo-, 1-аРК„];

аРКо + aQo+O - ccPio) «"1 aQBK„ + aQ(l-aPKo)Ki 1 - аРКо

Последнее выражение показывает, что в конечное состояние равновесия систему можно перевести за два периода прерывания мгновенного ключа. Для этого необходимо совместное выполнение вух условий:

XI (2/1) = а (Р + Q2) аР (1 - аРКо) Ki=l; xt (2ft) = aQBKo + aQ (1 - aPK„) Ki = 0.

Из условий (1.4), используя выражения (1.3), записываем

a{P-\-Q-BP]

ah{l -В)

1 - аР/<о

а[1~£(1 +bh)]-

(1.4)

(1.5)

Определим передаточную функцию цифрового регулятора на основании выражения (1.2)

W (г) =

Каи(0*)+КуЩ т г-

M,(0+) + M2(ft)2-i где И2(0+)=1; Oj = (ft+) = 1 - аР/Со =

I - Д (1 + bft).

>

bh (1 - В)

Ь, = «2 (ft") = - JB: в = е-*".

Из выражений (1,5) и (1.6) видно, что коэ(}х})ициенты передаточной функции цифрового регулятора можно определить непосредственно через параметры передаточной функции объекта регулирования и шаг квантования й.

Оптимальный цифровой регулятор (при единичном ступенчатом воздействии на входе системы) формирует следующие управляющие воздействия на входе объекта регулирования: /По = н2 (0+) = Ко; nil = «2 Ф*) = <1«2 (h+) = - ВКо- Переход-