Кратко рассмотрим численный способ определения выходной координаты объекта регулирования х (О, которая является выводи ой координатой системы на рис. 1.1, а.

Уравнение идеального интегрирующего звена имеет вид

x(0 = 5«(T)dT.

Это уравнение можно преобразовать в разностное с помощью дискретизации. Для малых шагов квантования непрерывное интегрирование можно заменить численным интегрированием, например, по методу трапеций:

где л:„ = ж (пАо); «п = и (яЛо); п = О, 1, 2, ...

Этот алгоритм вычисления интеграла является нерекуррентным. Для программирования на ЭВМ более удобным является рекуррентный алгоритм, который получается следующим обра-еом. Запишем предыдущее значение переменной х

и найдем разность Тогда

Выражение (1.71) представляет собой рекуррентное разностное уравнение, определяющее связь выходной и входной переменных для интегрирующего звена.

Для апериодического звена на основании формулы (1.71) запишем еледующие соотношения:

Хп ~ + + *n«-.l) • Хп = и„ - Ьх„,

из которых находим

2-% , ftp , , "

= 2 + Шо """-i + 2 -f ЬЛо + "п--

Аналогичным образом, используя выражение (1.71), можно получить рекуррентные разноетные уравнения для колебательного, консервативного, форсирующего и других линейных ди-намичееких е1веньев, из которых состоит математическая модель объекта регулирования. Такие разностные уравнения для различных звеньев приведены в табл. 1.3. Составляя линейную математическую модель объекта регулирования в виде комбинации

!.3. Рекуррентные формулы для расчета непрерывкой части систем (по методу трапеций)

Тип звена и его передаточная функция

Схема в переменных состояния

Рекуррентные формулы

Интегрирующее I

Апериодическое . 1 s + b

Колебательное 1

.s-{- bs + a

+ 2+ +

i - 2bha~ahl

. 4 + 26fte-faft

X«in-i+

2fco

+ 4 + 2bfto+«ftr""" «14== *ln-l + "2" (-"йп-Ь

Форсирующее sj-d s + b

2-% + 2T№o"" + ""->=

*:iB=Mn--(i -b)A;g„

продолокение табл. 1.S

Тип звена и его передаточная функция

Схема в переменных состояниях

Рекуррентные формулы

Консервативное 1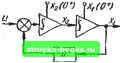

2ft„

2 •»lrt l+

2 «n-i);

4 + aX

Xln-Xln-1+ -2<.X2n+X2n-j)

различных линейных динамических звеньев, с учетом табл. 1.3 можно легко вычислить выходную координату объекта регулирования X (<) при поступлении на вход объекта управляющих воздействий m (fj и различных начальных значениях Х(, = х (О""") и «о = « (О*) переменных состояния каждого звена. Шаг квантования hg при численном интегрировании должен быть значительно меньше шага квантования h мгновенного ключа в системе на рис. 1.1, а (обычно h = (50...100) h) и на порядок меньше наименьшей постоянной времени объекта регулирования для получения высокой точности расчетов. Рассмотрим конкретные примеры.

Пример 1. Математическая модель объекта регулирования в системе на рис, 1,1, а описывается передаточной функцией

G (S) = а [S (S + а) (s + b)]-\

где а = 800 с"; с = 20 с""-; b = 2 с"*. Шаг квантования мгновенного ключа в системе на рис. 1.1, а ft = 0,1 с.

Для заданной передаточной функции G (s) объекта регулирования по табл. 1,2 (п. 9) находим z-изображение оптимального управляющего воздействия

Al(z) = Ko(l-f 6iZ-J + V-=) = = 3,19005 (I - 0,954072-1 + 0,11080z-2).

Таким образом, на выходе цифрового регулятора должна быть последовательность мгновенных импульсов с периодом следования h, площади которых т,, = т (О*) = Ко = 3,19005; mi= = т (ft-) = biKo == -3,04352; = m (2ft+) = bKo = 0,35347, или на входе объекта (после фиксатора нулевого порядка) должна быть последовательность импульсов, имеющих одинаковую длительность ft, но разные амплитуды, соответственно равные то, «1, Щ.

По управляющему воздействию на входе объекта m (/) и передаточной функции объекта регулирования G (s) определяем выходную координату объекта (выход системы на рис. 1.1, а) х {i) и ошибку в системе & {f) = I - х (t). Выходная координата си-

8 8-224 65