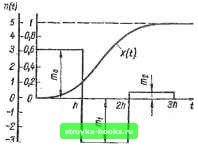Рис. 1.12

стеыы и управляющее воздействие на входе объекта регулирова-кия изображены на рис. 1.12. Определив ошибку 0 (vft+) = & (fj при t = vft", V = О, 1,2..., на выходе мгновенного ключа в системе на рис. 1.1, а, запишем передаточную функш1ю оптимального цифрового регулятора согласно выражению (1.70)

Ш,,,--, юпп 1 -0.95407г-1 + 0.11080г-2 W (г) - d,19005 J о.76955г-1 + 0.10761г-2 •

Пример 2. Математическая модель объекта регулирования в системе на рис. 1.1, а описывается передаточной функцией G (S) = а [S (S + с) (s2 + bs + «)]-!, где а = 10* с"»; с = 10 с"!} b = 1 с-1; а = 2 с"". Шаг квантования мгновенного ключа в ей-

стеме на рис. 1.1,в ft=0,l с. 4Щ Для заданной переда-

точной функции С (s) объекта регулирования из табл. 1.2 (п.26) находим г-изображение оптимального управляющего воздействия

M(z) = Ko{l+biZ-i + + &2г-2 + 6зг-«) = = 1,6652 (1 -2,25372-1 + + 1,59862-2 -0,3329г-8).

Таким образом, на выходе цифрового регулятора должна быть последовательность мгновенных импуль-сов с периодом следования /г, площади которых тд = т (0) = = Ко = 1,6652; mi= т (ft+) == bKo = -3,7528; ma = m (2/г+) = = fcaKo = 2,6619; mg = m (3ft+) == fcgKo = -0,5543, или на входе объекта (после фиксатора нулевого порядка) должна быть последовательность импульсов, имеющих одинаковую длительность ft, но разные амплитуды, соответственно равные щ,, Щ, mg, пц.

По управляющему воздействию на входе объекта т (t) и передаточной функции объекта регулирования G (s) по изложенной методике определяем выходную координату объекта (выход системы на рис. 1.1, я) л; ( и ошибку в системе © ( = = 1 - X {{). Выходная координата системы и управляющее воздействие на входе объекта регулирования изображены на рис. 1.13. Определив ошибку системы 0 (yh*) = 0 {t) при t = vft*, V = 0,1, 2... на выходе мгновенного ключа, запишем передаточную функцию оптимального цифрового регулятора согласно выражению (1.70)

W,.- fifiW 1 -2.25372- + 1.5986;-2 -0,3329г-« W \z) - 1,000 J 0,95222-1 + 0,47072-2+ 0,0371г-з *

Пример 3. Математическая модель объекта регулирования в системе на рнс. 1.1, а описывается передаточной функцией G (S) = а [S (S+G) (S + Ь) (S+C) (S + d) (S + g) (s + П] \ где а= = 106 с-?; а = 0,5 с""-; 6 = 1 c-i; с = 2 c-i; d = 10 c-i, g == - 100 с"!; f= 200 с-1. Шаг квантования мгновенного ключа в системе на рис. 1.1, а й = 1 с.

Для заданной передаточной функции G (s) объекта регулирования по табл. 1.2 (п.52) находим г-изображение оптимального управляющего воздействия

М (г) = Ко (1 + biz- + Ьг- + Ь- -f + 642-* -f bf,z- -f бог-") « 9,30018 (1 - l,10979z-i -f -f 0,35505z-2 - 0,0302142-3),

где коэффициенты b, fcg и fc пренебрежимо малы.

Таким образом, на выходе цифрового регулятора должна быть последовательность мгновенных импульсов с периодом сле-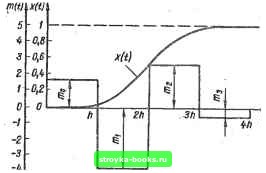

Рис. 1.13

дованияЛ, площади которых Шд - т (О*) = Ко = 9,30018; mi= == т (ft) = fciKo.= -10,32125; ==m {2h=bKo = 3,30205; /Из = m (3ft") = йзКо = -0,28099, или на входе объекта (после фиксатора нулевого порядка) должна быть последовательность импульсов, имеющих одинаковую длительность h, но разные амплитуды, соответственно равные т, т, т, Шд.

Выходная координата системы и управляющее воздействие на входе объекта регулирования изображены на рис. 1.14. Определив ошибку системы 6 (vh) =1 - х (yh*) на выходе мгновенного ключа, запишем передаточную функцию оптимального цифрового регулятора согласно выражению (1.70)

1 - 1,109792-1 + 0,355052-= - 0,0302142-3 W (2) = 9,30018 J o,94I51z-i -f 0,41545г-2 -f 0,02846г-з *

На основании расчетов можно заключить, что в данном случае дискретная модель объекта регулирования при принятом шаге квантования h и указанных частотах сопряжения имеет не седьмой, а четвертый порядок.

Изложим еще одни способ определения передаточных функций W (г) оптимальных для ступенчатых воздействий на входе системы рис. 1.1, а цифровых регуляторов [31]. Обозначим входную и выходную координаты системы и выходную дискрету цифрового регулятора в момент времени t = vft" соответственно и (vA+) = « (v); X (vft+) = X (V); т (vft+) = mv~ т (у).

При единичном ступенчатом воздействии на входе системы рис. 1.1, а с оптимальным цифровым регулятором справедливы

3* 67

следующие соотношения: х (v) - и {\) == I к т (\) = т (N) для V > N, гце N - порядок полинома в знаменателе передаточной функции G (s) объекта регулирования.

Используя г -преобразования для последовательностей и (v), X (v), т (V) при V = О, 1, 2, .... запишем

Х(г) = x(\)z- + x(2)z-+----h г-" (1 + z"! + z"" + ...)}

M{z) = m(0) + mЦ)z--\----

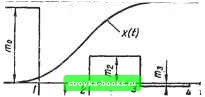Рис. 1.14

(0) + m(I) ----+ m(iV - 1) 2-+

при статических

М(г) -т

при астатических объектах регулирования.

Допустим, что дискретная передаточная функция объекта регулирования с фиксатором нулевого порядка при заданном шаге квантования h определена и имеет вид

X (2) Ci2-i + cz- -f • • -f сг- /0() = л77;Т=.. , ,-Г-Г-ГГГ. (1-72)

М (г) 1 + djz-- + dz- +

Определим дискретную передаточную функцию замкнутой системы (см. рис. а) в виде

W(z)HG(z) X(z)

Лз - 1 + W (2) НО (2) ~ <У (2) ~

где ki==x (I); = л: (2) - л: (I); ... = I - л: (ЛГ - 1). Отметк-м.

чго fei-f + •• - -f A;v = 1-

Запишем отношение z-преобразований

1/(2)

= <2 (г) = Ко (1 + 6x2-1 + 622- + • • • + bjz-).

где Ко = т(0); Кох

= т (1) -т (0); ... Kji = m -1)-.