где Р (t) = - fftT - 1 + В (т)1; Q (т) = 1 [1 - В (т)]; В (т:)=е

Переходные процессы в интервале 0+ <: т < й, ft+ < < 2Л, i = T-{-h, определяются вектором

"а [Р + QQ (т)] /По + аР (т) пц B(T)= a,QB(x)mo + aQ{T:)mi L «1

(1.80)

Пусть объект регулирования в системе на рис. 1.2, а имеет параметры а = 10 с~"; b = 2 с . На вход системы поступает входное воздействие и (/) = 1 + 2/, т. е. U - I, а - 2 с~К Определим передаточную функцию оптимального цифрового регулятора при шаге квантования /г = 0,1 с. По формулам (1.76)-(1.78)

14,3066 - 23,8131 г-1 + 9,906б2-«

W(z)

(1 - г-1)(1 4-0.53012-1)

-loL

. Переходные процессы в системе на рис. 1.2, а, рассчитанные при заданных параметрах объекта регулирования и цифрового регулятора по формулам (1.79) - (1.80), показаны иа рис. 1.15.

Определим передаточную функцию W (г) оптимального цифрового регулятора для системы на рис. 1.1, я с объектом регулирования, математическая модель которого описывается передаточной функцией G (s) = aJs\ при поступлении на вход системы воздействия « (f) - U а/. Эта передаточная функция имеет вид

Ьп + 6i2-i

1 и h

°t = t~ + To-

t; 3 и

где 6о = 2 + 1 =

Переходные процессы в интервале 0+ < т < ft, / = т, определяются вектором

г.(т):

, Переходные процессы в интервале 0+ < т < ft, Л+ < / < 2/i. / = T4-ft, определяются вектором

Пусть объект регулирования имеет параметр а = 10 с- На вход,системы (см. рис. 1.1, а) поступает входное воздействие и (t) - 1 + 2/, т. е. и - 1, о = 2 с Определим передаточную функцию оптимального цифрового регулятоза при шаге квантования й = 0,1 с ио формуле (1.81)

где Ьо = 10 + 1.5о; Ь = -10 - 0,5а; = 0,5 + 0,025а.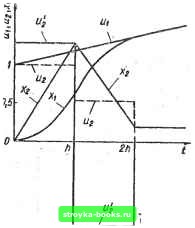

Рис. 1.16

Переходные процессы в системе на рис. 1.1, а, рассчитанные при заданных параметрах объекта регулирования и цифрового регулятора, показаны на рис. 1.16.

Передаточная функция W (г) оптимального цифрового регулятора для системы на рис. 1.1, а с объектом регулирования, математическая модель которого описывается передаточной функцией G (s) = a/s, при поступлении на вход системы воздействия u{f) == и + ot имеет вид

6л =

и

afts + 2ft и

(1.82)

U J

fli =-g-+-3-a; aj =-g-+-g a.

Переходные процессы в интервале 0+<T<;ft, t = i определяются вектором

(1.83)

(1.84)

Переходные процессы в интервале 0+<!T<ift, A*<!<<2/i, f = т -f- /J. определяются вектором

«(1)= --а/126о4-аЛт6о + 4-«г1 a/i6o 4- arfcj

Переходные процессы в интервале 0*<:T<:ft, 2/i+<j<!3ft, < = т 4" 2/г определяются вектором

- сЛЧо 4- o/xSfti 4-1- оЛЧбо 4- у СсЛЧб! 4-

4- сЛтбо 4- - аЛтб 4- ата

3 1 1

Y oth4o 4- -g- аЛг»! 4- ahibf, 4- аЛтб 4-ахЧ

ahbf, 4- aftbj 4- атб,

Пусть объект регулирования имеет параметр а = 100 с". На вход системы (см. рис. 1.1, а) поступает входное воздействие « (О = I + 21, т. е. и = 1, о = 2 с-1. Определим передаточную функцию оптимального цифрового регулятора при шаге квантования ft = 0,1 G по формуле (1.82)

4-26г-14-12г

5 1

где йо=104-2(т; 6i=-20 -Зо; 62=104-0; ai=- + ja;

г.(г):

.(1.85) .

Т + бо"-

Переходные процессы в системе на рис. 1.1, а, рассчитанные при заданных параметрах объекта регулирования и цифрового регулятора по формулам (1.83) - (1.85), показаны иа рис. 1,17.

Рассмотрим систему на рис. 1.1, а, в которой математическая модель объекта регулирования описывается передаточной функцией С (s) = а [s {s 4- я) (s 4-6)1 Схема аналогового моделирования для объекта изображена на рис. 1.6, а. Дискретная матрица перехода для объекта имеет вид

~1МР aL" OA WaP 0 0 В aQ 00 О 1

где элементы матрицы определяются выражениями (1.9), (1.21). Оптимальные переходные процессы в системе на рис. 1.1, а с таким объектом регулирования при ступенчатом входном воздействии исследованы ранее (см. формулы (1.21) - (1.26), (1.40), (1.41)). Некоторые результаты этих исследований используем ниже.

0(ft):