При поступлении на вход системы на рис. 1.1, а о рассматриваемым объектом регулирования линейно изменяющегося воздействия и (t) = и + oi при нулевых начальных условиях можно организовать переходный процесс без перерегулирования выходной координаты за минимальное время, равное ЗА, если выполнить совместно три условия;

Хх (ЗА) =a(L + MP + PQ + AMP + MWQ + BQP) ntg +

+ all+ PM + QP) mi + aLm = i/ -f ЗЛа;-(ЗА) = a (AP + AWQ + BWQ)mo + a (AP + QW)mi+ (1.86) aP«2 = a; лгд (ЗА) = aQ {Bm„ -f Bmi + /wj = aa.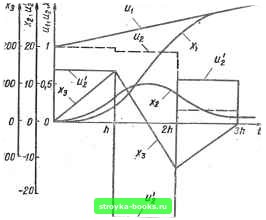

Рис. 1.17

Записанные уравнения отличаются от уравнений (1.40) правыми частями, что приводит к более сложным математическим выкладкам при решении системы уравнений (1.86). Умножая второе уравнение на q, а третье уравнение на Р и вычитаяиз второго уравнения третье, после несложных преобразований находим следующее соотношение;

Q - aP

mi = -(Л + В) то + aQ(AP + QW=W) °-

Используя выражения (1.9) и (1.21) для элементов дискретной матрицы перехода Ф (А), получаем

mi = -(Л + В)то +

7А)(Г~)0- (»-87)

Умножая второе уравнение на BQ, а третье уравнение - на (АР -f- QW) и вычитая из второго уравнения третье, после несложных преобразований имеем

а(АР + QW) - BQ т = АВто + fjp .. qr/ ВР) °-

Используя выражения для элементов дискретной матрицы перехода Ф (А), определяем

ab(l -A~B)

Подставляя значения nii и «а из формул (1.87) и (1.88) в первое уравнение системы уравнений (1.86) и используя выражения для элементов дискретной матрицы перехода Ф (ft), решаем это уравнение относительно неизвестного

ah О- -А){\ - В)

h a + b\ Л -Т=В+~5Г] ° •

\ - А

(1.89)

Подставляя выражение для величины в формулы (1.87) и (1.88), находим

ab (А -f В)

ah{\-A)(\-B) ft

A~\-B

~ A + B

ab AB Г /о. A A A.

-aft(l-A)(I-B) [t + \3ft- B+ AB-

. ft ft a + b\

~l-A-l-B+ ab }°

(1.90)

(1.91)

В установившемся режиме . ..•

m = ~(j при v>3. (1.92)

Таким образом, оптимальный цифровой регулятор при линейно изменяющемся входном воздействии должен формировать управляющие воздействия на входе объекта регулирования

в переходном режиме «о = "а Ф*У> т1=щ (h*); «а = "а (2*). которые определяются выражениями (1.89) - (1.91), и в установившемся режиме - управляющие воздействия, которые определяются выражением (1.92) и образуют постоянную величину на входе объекта.

Найдем последовательность импульсов на входе цифрового регулятора:

«а (ft*) = f/ + fto - xi (ft+) = U +ha - aLnio +ha - X

bA - aB

abh~(,a + b)+

J (2ft+) = t; + 2ft(j - % (2ft*) = {/ + 2fto - d [(L + + PQ

+ Lm,J = t; + 2fto-{

a6ft +

6M(1 - Л) -o2B(I -B)

a - b

aB - 6M7

+ [aftft-(a + ft)+ J

(1.93)

(1.94)

Передаточная функция оптимального цифрового регулятора

w м - «о + тг"! + mz- + т, (г"» + г + ... + г" + .. .)

- (1-Z-1) (t; + Oiz-i + az-) l-9>

где bo = m; bmi- moi bm- m,; = -«г! = «гС*):

fl2==«2(2ft+).

Определим переходные процессы в системе на рис. 1.1, о с рассмотренным объектом регулирования и оптимальным цифровым регулятором, обеспечивающим минимальное время регулирования, равное 3/г, без перерегулирования выходной координаты X (f) при линейно-изменяющемся входном воздействии « (О = и + of.

Переходные процессы в интервале О* < < < ft, / = т, определяются вектором

v (т) = [xi, х; Xg-, т] = [aL (т) Шо; аР (т) Шо,

aQ(x)mo: Шо], (1.96)

где L(T)=

ЬА (т) - аВ (т)

абт -(й + &) +

ЬЫ (т) - аВ (т)

/(x) = ix

1-f-

, (1.97)

a-b J Q()=tH-B(T)]; A(r) = e--B{%) = e-.

Переходные процессы в интервале h* 2h, 0+ < т < ft, / = T -f- A, определяются вектором

г a [L + PjM (T) + QP (т)] Шо + aZ, (т) т а ГРЛ (г) + QW (т)\ то + аР (т) т aQB (T)mo + aQ(T)mi mi

где Ж (т) = [1 - Л (т)]; W (т) = [В (т) - Л (т)}.

Переходные процессы в интервале 2ft+ <: Г<: 3ft, 0+ <: т <: ft = т + 2ft, определяются вектором

а (L + РЛ-г + QP) то + aLm + а [(ЛР -f" + Q то + Pmi\ М (т) + а {BQmo + + Qmi)P(T) + aL(T)/n, ф (т) = а [(ЛР + Q W) то 4- Рт] Л (т) + . (1.98)

-f а (BQmo + Qx) (т) + « (т) а (BQmo + Qi) В (х) + aQ (т) т

Рассмотрим пример. Пусть параметры объекта регулирования а = 800 с~; b - 2 с-1; а = 20 С. На вход системы на ркс. 1.1, а поступает воздействие и {() - U +о<, где U = \, о = 2 с-1. Определим передаточную функцию оптимального цифрового регулятора при шаге квантования ft = 0,1 с по формулам (1.89) - (1.95):

4,35559 - 7,87309г-1 + 4,029432" - 0,41193г-8 (1 2-1) (I + 0,842972-1 + 0,10292г-2) "

Оптимальный цифровой регулятор формирует на выходе Б переходном режиме последовательность мгновенных импульсов,