гоо too

-too

V7,S-US\

.-2,51

7"

Рис. 1.19

}Хф*)

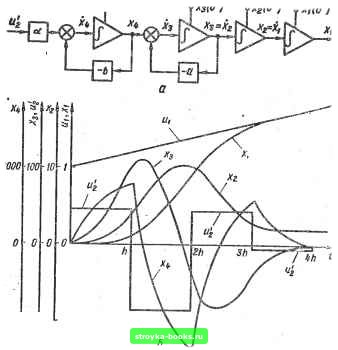-тоЧооио

Рис. 1.20

= «2 (A+), 1712 = ul (2/г*). Для заданных параметров объекта регу» лирования и шага квантования получаем следующие значения: «о = 1.37916[/ + 0,27354а; mj, = -2,50833[/ - 0,35957а; т, = == 1,12916[/+0,11104а, где £/ = 1, а = 2 сК

Переходные процессы в системе иа рис. 1.1, а с указанным объектом регулирования и оптимальным цифровым регулятором при входном воздействии и (t) = 1 + 2< и нулевых начальных условиях, рассчитанные по формулам (1.108) - (1.110), изображены на рис. 1.19.

Рассмотрим систему на рис. 1.1, ас объектом регулирования четвертого порядка, математическая модель которого описывается передаточной функцией G (s) = а [s (s+ а) (s + Ъ)]~. Объект регулирования имеет астатизм второго порядка. Схема аналогового моделирования для объекта изображена на рис. J.20, с. Дискретная матрица перехода для объекта имеет вид

г1 hS L ccGn О 1 Ж Р aL 00 А WaP ООО В aQ

0(h) =

-1+Л);

Loo О

{a + b)h

gg + ab-f i

a остальные элементы матрицы перехода определяются по формулам (1.9) и (1.21).

На вход системы на рис. 1.1, ас рассматриваемым объектом регулирования поступает линейно-изменяющееся воздействие и (О = и + at при < > О и нулевых начальных условиях. Определим передаточную функцию W (г) цифрового регулятора, обеспечивающего оптимальный переходной процесс х (Q.

Обозначим «2 (vh*) = m, v = 0. 1, 2, ... и найдем значения вектора v = \Xi, х; Хд; х; т\ в дискретные моменты времениг

«(0+) = ]0; 0; 0; 0; /Ио1

о" (ft*):

о (2ft+) =

laGmo; aLnifii аРт; aQm„; mi\; га (С + ftl, + PS+ QLfnio + oGmi-i a (L + PM + QP) Шд + al,mi a(AP + QW)ma + aPmi aBQnig -j- aQmi

ff?2

D (3ft+) = ( C; D", Ei F; ,

С = a\GJrhL + PS-\-QL-Yh(L + PM + QP) + S(AP + QW) +

+ BQI,] «0 + «(G + hL + PS + QL) + aGm; D=a [L + -b PM + QP + Ж (АР + QW) + BQP] mo + ce (L + РЖ + QP) mj + --aLma; E = aiAP+AQW + BQW)mf, + a(AP + QW)mi-b -i- aPm; F = aBQm + aBQm 4 aQm\

rC + hD + SE + LF + aGmg-D + ME+PF +aLms AE + + aPms BF* + ceQma

© (4ft+) =

Чтобы переходные процессы в объекте регулирования при нулевых начальных условиях заканчивались за время, равное 4ft, необходимо равенство вектора v (4ft+) вектору = U-\-+ 4Ла; а; 0; 0} О . Составляя систему уравнении v (4ft+) = и решая ее относительно неизвестных т, т, щ и т, получаем следующие окончательные результаты:

«1 =-«о (I + ++ ЩП1Т1=) /п, = то (Л + Д + т - (fij"(fi. о; > (1.111)

аЬАВ

щ = -тоАВ + (, а:

ай2(1-Л)(1-В) Г +

4ft-

5ft - 3ft (Л + В) + ftЛв

2 (1 - Л) (1 - S)

Определим входные дискреты цифрового регулятора e(G*) = t/ -л:1(0+) = [/;

©(ft*) = ai + fta -(ft+) == [/ + fta - oGmo = f/ + ft2 (c + 6>ft

(1-Д) -fe(t -Л)

(1,112)

(1.113)

2 aft 1- • аЧ{а - Ь)

e (2ft+) = og = [/ + 2fta - (2ft+) = С/ + 2fta - a (G-f ft! + PS +

+ (2I.)m„-aGm, = f/ + 2fta-{[

d>B (1 - B) - 6M (1 - Л)]

+ «262(0-6) J+

дз (i - В) - fcs (1 A).

ab (a + b)h

e(3ft+) =t/ + Sfta-j{

(a-b)

Оз = [/ + 3ft a - (3ft+) = [/ -f 3fta - С = 5ft htja + b) азд (i:-в) бз2 (i-Л)

(1.114)

a262 (Я b)

3ft2

ft (fl + fe) g»B(l - B)-6ЭЛ(1 - Л)

«1 +

c6 "T- аЧ(а - Ь)

(a + fc)ft дЧ1-Д)-г"(1-Л)1 .

+ [2~ OA + аЧ{р - Ь) J"4* *

Передаточная функция оптимальнога цифрового регулятора (см. табл. 1.4, п. 9)

где 6о = "о; f>i = mi; Ь-щ; Ь - щ.

Оптимальные переходные процессы в интервале О* < / < ft, = т, определяются вектором

(т) = I aG (т) <xL (т)тд; аР (т)«оГ

aQ(T)mo;mo, (1.117)