
 |
|
Главная Система автоматического управления [0] [1] [ 2 ] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] . ные процессы в интервале 0+<:/<:/г, / = т, определяются вектором . (т) = [1; аР (т) Яо; aQ (т) К; 1]. (1.7) Р (т) = [Ьх - 1 + В (т)]; Q (т) = у [1 - В (т)]; В (т) = е. Переходные процессы в интервале <.t<2h, 0+ <: т А t = x-\-h, определяются вектором * аК [QB(T)-BQ(T) 1 -aP/fo (1.8) Пусть объект регулирования имеет следующие параметры: b - = 2с-1, а= 10с-2,/г = = 0,1 с. Определим передаточную функцию цифрового регулятора, обеспечивающего оптимальный переходный процесс в системе, т. е. оптимальную реакцию на выходе системы, при подаче на вход ступенчатой функции по формулам (1.5) - (1.6) Г (2) = 1-0,81в7г- = 11,0333 J 4533-1. Переходные процессы в системе, рассчитанные по формулам (1-7) и (1.8), изображены на рис. 1.2,6. Наиболее просто по изложенной методике определить передаточную функцию W (г) цифрового регулятора для системы (см. рис. 1.1, а), имеющей объект регулирования второго порядка с передаточной функцией G (s) = ct/s [22]. Схема аналогового моделирования для такого объекта показана на рис. 1.3, а. Оптимальную передаточную функдаю цифрового регулятора можно вычислить по формуле (1.6), в которой Ко = l/{ah); Ki =~2Kt= =i -.2/(аЛ2); (0+) = 1; 6i = Kx«2 (h*)/K„ = - 1; «1 = Mj, (A) = 1-аЛ2/с„/2=1. т.е. 1 l~г- "(2)= ah 14-0,52-1 • 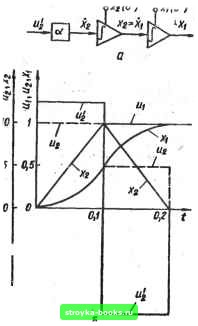 •S Рис. 1.3 Оптимальный цифровой регулятор формирует следующие управляющие воздействия на входе объекта регулирования: т„ = (0+) = /<о = 1 Kahy, mi = и (/i) = Kiti (h+)=- 1 /(ah). Переходные процессы в интервале 0*<:#<ft, t = x, определяются вектором »Мт) = К; X,; X,; и]=1\; гУ(2к); 1].  20 10 0,5 О*- О
0,3 t Рис. 1.4 Переходные процессы в интервале ft* < < < 2ft, 0+ < т < It, t=x-\-h, определяются вектором да(т) = [1; 1/2+Т/& -TV(2ft2); 1/ft-T/ft2; 1/2]. Переходные процессы в системе (рис. 1.1, а) при а = 8 с" и ft = 0,1 с изображены на рис. 1.3,6. Передаточную функцию цифрового регулятора 15?(г) для объекта, имеющего передаточную функцию G (s) без интегратора, определить сложнее. В этом случае цифровой регулятор должен выполнить интегрирование, и его передаточная функция усложняется. Рассмотрим систему (см. рис. 1.1, а), в которой математическая модель объекта регулирования описывается передаточной функцией G (s) = а [(S + о) (S Ч- fc)]Объект регулирования имеет астатизм нулевого порядка. Схема аналогового моделирования для такого объекта изображена на рис. 1.4, а. Запишем дифференциальные уравнения состояния для системы иа рис. 1.1, бс этим объектом регулирования (без учета переменного коэффициента усиления К): = 0: х - х~ ах; = о.щ - - ЬхЦ «2 = 0. Уравнения переходных состояний имеют вид «j (vh+) = «1 (v/i); xi (vh+) = a:i (vh); (vft+) = (vh); (vft+) = = «1 (v/г)-л: (v/г). Переписывая уравнения в векторно-матричной . форме V ~Av к V (vA+> = Bv (v/г), находим "О О 00 о -а 10 О 0-Ьа 0 0 00 : в = "1 ООО о 100 о 010 1-100
с учетом усилителя с переменным коэффициентом усиления определим дискретную матрицу перехода по матрице А в виде "10 0 о 1 о AW РКм 00 в aQK 00 О 1 = е-"; В = e-f>\ Г = (Л - В); (ЬА~аВ) ; (2 = (1-В). (1.9) Далее на основании соотношения (1.1) последовательно вычис- ляем о(0+) = (Во(0)) = [1; 0; 0; 1]; v(h) = (Ф (Л. /Со)о(0+)Г= [1; аР/Со; aQK; I]; •(Л+) = (Вг(Л))=[1; аР/Со; ctQ/Co; l-aPKY aP/Co+aQ/Coll7+aP(l - aPKo)Ki aQKoB + aQ (1 - aP/Co) 1 - aPKo V (2h) = Ф (h, Ki) V (A+) = Последнее выражение показывает, что в конечное состояние равновесия систему можно перевести за два периода прерывания мгновенного ключа. Для этого необходимо совместное выполнение двух условий; XI (2Л) = аРКоА + aQKoVi" -f аР (1 - аРК) 1 = 1П п " 10) х (2ft) = aQKoB + aQ (1 - аР/Со) Ki = а. ] Из условий (1.10), используя выражения (1.9), записьшаем Q - аР аЬ 0 = aQ (ЛР+ QW - BP) = а(1-Л)(1-В) a-aQBKo ab (а-b) (1 - А - В) i = aQ(l-aP/Co) - а[(а-й)Лб-аЛ + 6В]- •> При совместном выполнении указанных условий имеем v (vft) = о (vft+) = [I; 1; «; 0]; (vft+) == при v = 2, 3, 4,... [0] [1] [ 2 ] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] 0.0014 |