печит переходной процесс на выходе системы за минимальное время Nh, но перерегулирование этого переходного процесса может быть любым, в зависимости от параметров форсирующего звена.

Рассмотрим систему управления на рис. 1.1, а с объектом регулирования, математическая модель которого описывается передаточной функцией G (s) = а (s + d) [s (s + b)]". Пусть на вход системы поступает воздействие и {() = U -\- ct ш начальные условия в системе - нулевые. Схема аналогового моделирования объекта изображена на рис. 1.23. Запишем дифференциальные уравнения состояния системы:

= х, Х2 = dXg - с.«2 - Ьх; Xg = акд - Ьх; щ = 0.

Рис. 1.23

Переписывая уравнения в векторно-матричной форме в = Av, где « = [Xi, Xji, Xg, «2], определим дискретную матрицу перехода в виде

I h D аЕ

О 1 id~b)Q a(h + D) О О В aQ

ООО 1

где Q = j(l -В): D: ~2hb + 2 - 2B)+; B = e- (1.126)

{bh-l+B); £ =

d~i 263

{hb~

Обозначая u{\h*)=m, v = 0, 1, 2 .... последовательно

находим

V (2ft+) =

V (3ft*) =

«(0+) = 0: 0; 0; mj; v (ft*) = I аЕшо, a (ft + D) 1щ; aQm; [;

с. (£ + ft2 + ftD + DQ) ffio + a [ft + D + (d - 6) Q2] 4. a (ft 4. D) mi aBQtria + aQmi mg

a{E + 2ft2 + 2ftD Ч- DQ + ft (d - 6) + bQD\+ + a (£ Ч- ft2 + ftD + DQ) mi + aEm,

a[ft-f D + (d-6)(l+B) Qmo + a[h + D + + (d - 6) Q2] + a (ft + £>) m;

aBQm 4. aBQmi + аС1щ

в конечное состояние систему можно перевести за три периода прерывания мгновенного ключа (за 3 h), если выполнить следующие условия:

xi (ЗА+) = f/ -f- Зйа; % (Зй+) = о; лгд (ЗА+) = О

Иа (3/г+) = ms = 0. Решая систему уравнений (1.127), находим

ahd(l -В) ЬВ

тВщ-с-щ-у,

Ь Г.. /5й ft 1 iV в - аНЧ (1-В) + V"2 - rz-g + "F - j

(1.127) (1.128)

(1.129) (1.130) (1.131)

Подставляя выражение (1.131) в (1.129) и (1.130), оконча-

тельно Находим

Ь(\+В) --dh4(l-B)

и + 0

(&i h \2 ~l-B

= аНЧ (1 - В)

.+4-r=B+T-d-jj

i + Bjy

(1.132)

, (1.133)

Определим входные дискреты цифрового регулятора:

е(о+) = г/-л;1(о+) = г/;

0 (Л+) = U + ha - Xx (ft+) = f/ + fta - - (ft262 2ft6 +

+ 2 -2B)+ft2

(1.134)

0(2Л-

= U + 2ha

\d -

= U+2hp~Xi(2h*)

3rfft2 2(d-~ b)

(6ft-B + B2)Jmo +

[ti4 - 2bh+2 - 2B)+h tn. (1.135)

Передаточная функция цифрового регулятора (см. табл. 1.6, п. 1)

п7/,ч Ьр + Ьг- + Ьг-

где коэффициенты 6(, = то; bi - irii; Ь - т; Gi=0(ft+); Оа = = ©(2/i+) можно определить по формулам (1.131) - (1.135).

Переходные процессы на выходе системы (см. рис. 1.1, а) с рассмотренными объектом регулированиями цифровым регулятором при параметрах а = 10 с fc = 5 с , шаге квантования А = 0,1 с, нулевых начальных условиях и воздействии на входе И (О = 1 + 2/, t/ = 1, а = 2с-1 показаны на рис. 1.24, а для

указанных значений параметра форсирующего звена d. На рис. 1.24,6 показаны переходные процессы иа выходе системы (см. рис. 1.1, а) при параметрах а= \0с~, b = 2 с~, шаге квантования h = 0,1 с, нулевых начальных условиях и единичном ступенчатом входном воздействии.

Рассмотрим систему управления на рис. 1.1, а с объектом регулирования, математическая модель которого описывается передаточной функцией G (s) = а (s + d) [s (s + a) (s + b)] . Пусть на вход системы поступает типовое воздействие « (О = = и ctn начальные условия в системе - нулевые.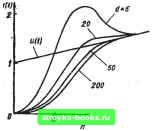

гл 31: i в

Рис. 1.24

Рис. 1.25

Схема аналогового моделирования объекта представлена на рис. 1.25. Запишем дифференциальные уравнения состояния для системы! = лга; х = ащ + (d - Ь)хд - ах; Хд = аи - bxi = 0. .

Переписывая уравнения в векторно-матричной форме v = Av, где v = % Хд, Из}, определяем дискретную матрицу перехода в виде

I М R аР О А W a{R + M) О О В aQ ООО 1

Ф(Л):

где А = 6-°"; В = е- М = Ц- ; Q

В-А а - Ь d - l

j[ ЬА - аВ V+ а-Ъ )

аВ - ЬЫ abh-(a + b)+ f,

ah-I-{-А