
 |
|
Главная Система автоматического управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [ 37 ] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] ляющие воздействия на объекты регулирования Шр, т, раи-ные по величине. Определим оптимальные управляющие воздействия, формируемые цифровыми регуляторами при неравномерном шаге квантования в системе иа рис. 1.2, а с объектом регулирования второго порядка. Пусть при поступлении иа вход системы единичной ступенчатой функции и при нулевых начальных условиях е выхода регулятора на вход объекта регулирования и интервале длительностью ho поступает управляющее воздействие /По, а в последующем интериале длительностью ftj поступает воздействие щ. По известной дискретной матрице перехода для объекта регулирования, используя описанную выше методику, последовательно запишем (fto) = {Ф (К) V (0+))"= I а Ррпго; аСоо; Щ I; i> {fO = I аРо«о; aQ/По; ; аРо/По + QaQio + аРт aQaBirria + aQi/nj Условия, при которых в системе на рие. 1.2, а переходные Ороцеесы вакаичиваются за два указанных, шага" квантования, Ч {К + hi) = aPoffJo + aQoQimo + аР-щ = 11 Ч Фо -f fti) = aQoBmo + aQimt = 0. Решая записанную систему уравнений, находим " «1=-&В1«о = -Цтгж«о: (1.146) 1 ЬЦ-Вг) oclfto(l-Bi)-Mi(l-Bo)l (1.146) Из уравнения (1.145) можно найти условие, при котором /no=/ni = /n = (l-Bo)fii=l-Bji или l g«M.(2 e-M.j0. (1.147) При выполнении условия (1.147) шаги квантования и ftj связаны соотношением Й1 = + уЬ(2-е**Ч а.И8) амплитуда управляющих воздействий Таким образом, в этом случае амплитуда 1управляющих воздействий зависит от разности шагов кваитоваиия Aft = fto-i = fto -ТпСЗ--Ч (1-150) Зависимости ftj = jf (fto) (сплошные линии), Aft = jF (ftj) (штриховые линии) и /па = jF (Aft), построенные по формулам (1.148)-(1.150) для различных значений ft, изображены на рис. 1.28. При малых значениях An значения величин hi и Aft также небольшие. Рассмотрим пример. Пусть объект регулирования в системе иа рис. 1.1, а имеет передаточную фуикщ1Ю G (s) = 0,2 [s (s 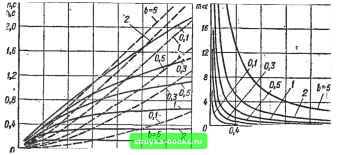 о,в 1,г ив uh,D В o,it 0,6 1,г ifi г,о г,4 л<,,с Рис. 1.28 -{- 0,5)]т. е. 6 = 0,5 и а = 0,2 с". На иход системы поступает единичное ступенчатое воздействие. Для получения оптимальных переходных процессов в системе цифровой регулятор с равномерным шагом квантования ft = 1 с должен сформировать два управляющих импульса с амплитудами: /По = 6 [aft (1 - е-*")]-! = 0.5 [0.2 (1 - еО-)]! « 6,35; = е--ЬЧ = -е"*"- • 6.35 = -3,85. Переходные процессы заканчиваются за время Т - Nh = = 2 с. Цифровой регулятор с неравномерным шагом квантования для интервала первого шага fto = 1 с должен сформировать интервал второго шага Л1 = 1п(2-е-°-5)=0, 6636 с. При этом Aft = fto - fti = 0,3364 с и амплитуда управляющих инпульсов « = б;2 0;3364 = Переходные процессы ваканчнваютая за время Т = fto-b •f hi s= 1,6636 с. 1.9. УЧЕТ НЕНУЛЕВЫХ НАЧАЛЬНЫХ УСЛОВИЙ ПО СКОРОСТИ В системах, имеющих оптимальные цифровые регуляторы для линейно-изменяющихся входных воздействий, но работающих при произвольных входных воздействиях, часто необходимо учитывать иенулевыз начальные условия по скорости. Рассмотрим систему на рис. 1.2, а, на вход которой поступает линейно изменяющееся входное воздействие вида и (i) •= = и + at, а вектор начальных условий ©(0+) = [xi(0+); xJO*): 4(0)] = [0; <о\ Щ]- Тогда a(P + Q)mo + Q(l+B)Co + aPmi aBQmo + Вс + aQmi v (2ft+) Учитывая, что в установившемся режиме при t>-2h значения выходной координаты и ее производной должны повторять входное, воздействие и его производную, т. е. = Нх = С + Cyt и Xi= = «х = Ох, определяем оптимальные управляющие воздействия на входе объекта из условий (2ft*) = (У -f 2ftai и х. (2ft*) = Ох- В результате получим п . 1 В nti = -Бто + Ох - с7о; и 2hQ - P "~a{P + Q - BP)~aQ(P + Q - BP) + вр-0(1+В) + aQ(P + q2 Bp)<Jo- Используя формулы (1.3), окончательно найдем ccft (1 - В) mi = Lu . b \ /1 ftBM (2Л + у - <i-[-b- Г=в/ "о ah (1 - В) b ~В(1 -В). В установившемся режиме "v~"a** >2. Поэтому г-изображение оптимального управляющего воздействия можно записать в виде М (г) = «о + тг- + х (г -f г"» -f • •. + 2 + • • •). Или М (г) =-Т~г где 6о = По; К = Щ - Щ\ bi = - Gi - mi. 11.6 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [ 37 ] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] 0.0012 |