
 |
|
Главная Система автоматического управления [0] [1] [2] [ 3 ] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] Таким образом, передаточную функцию цифрового регулятора можно записать в виде • iCo«2 (0+) + Л.ма (Л*) г-» + (г-" + + г-* + ...) W (г) = - «,(0+)+.м2(/1+)г-1 >(l-zTi)(l+ai?-i) - 01] ,-iv где i<2 (0+) = 1; ai = «а = 1 - аРАГо = (1.12) (a - b)AB - aA-{-bB {a - b){l -Л)(1-й) /5В. 6i = «2 (Л*)-«2 (0+)=-(Л + S); 6g = Из выражений (1.11) - (1-12) видно, что коэффициенты передаточной функции цифрового регулятора можно определить непосредственно через параметры передаточной функции объекта регулирования и шаг квантования h. Оптимальный цифровой регулятор при единичном ступенчатом воздействии на входе системы формирует следующие управляющие воздействия на входе объекта регулирования: гщ =«2 (0""")= = /Со; mi = ма (/г+) = f(iU(h) = (1 - Л - S) /Со: = «; (vA+)= ab = -npHv>-2. Переходные процессы в интервале 0+<<<й, / = т, определяются вектором фт) = [1: aP(T)/Co:aQ(T)/Co; П. где P(t)=-L ab ЬА (т) - аВ (т) :Q(i:) = (1.13) 1-е(г) М(т) = е-: S(T)=e «(T) = (1.14) Переходные процессы в интервале ft+ < < < 2А, О* < т < ft, f = т -f- ft определяются вектором аРКоА (т) + «Q/CoB (г) + {-- «e/C„)p(i;) aQ/Coe(i;) + --aS/Co) Q(i;) 1-аР/Со где й(1;)=[б(т)-/1(т)1. Пусть объект регулирования имеет параметры а = 10 с~, 6=2 c~, а = 20 с~. Определим передаточную функцию оптимального цифрового регулятора при шаге квантования Л = 0,1 с по формулам (1.11) - (1.12) 1 - 0,95407г-1 + 0,1 lOSOz (г) = 25,5204 (1 -г-1)(Ц-0,32794г-1) Оптимальные для ступенчатого воздействий Переходные процессы в системе (см. рис. 1,1, а) с указанным объектом регулирования, рассчитанные по формулам (1.13), (1.14), изображены на рис. 1.4, б. Рассмотрим систему (см. рис. 1.1, с), в которой математическая модель объекта регулирования описывается колебательным звеном с передаточной функцией G (s) = а (s + bs + o)- при условии, что 4а - fc2 >. q. Схема аналогового моделирования для такого объекта изображена на рис. 1.5, а. Запишем дифференциальные уравнения состояния для системы иа рис. 1.1, б с таким объектом регулирования (без учета переменного коэффициента К): Ux = = 0; ATj = дса; Х2<= = - Ьх2 - ах + a«g; «2 = 0. Уравнения переходных состояний такие же, как и для предыдущей системы. Перепишем дифференциальные уравнения в векторно-матрич-ней форме 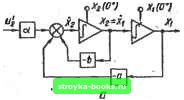 0.0 00 0 0 10 О -а ~Ь а О О 00
-o,s О
С учетом усилителя с переменным коэффици- • ентом усиления определим дискретную матрицу перехода "1 О О О О L М av О -аМ D аМК,, ООО 1 R = l I-VВ (coslh + :sm%hj ; (1,15) D==Yb (cos \h - Asin Aftj; Ji = /ЕБД; B=e* Далее на основании соотношения (1.1) последовательно вычисляем «(0+) = (£«(0)Г = [1; 0; 0; 1]: -о-" (Л) = (Ф (Л, Ко)«(0+)) = [1; aRKo; аМКо; П: «• = (В« = [1; aRKo; olMKo. i - «р/Со];. аМКоФ-аЩ+аМ{\-аНКо)К1 1 - aRKo В конечное состояние равновесия систему можно перевести за два периода прерывания мгновенного ключа, если выполнить Следующие условия: (xi (2ft) = a/Co (RL + Ж2) + a/? (1 - aRKo) /Ci = 1; ,6) К (2Л) = аЖ/Со (D - aR) + aAf (1 - aRKo) Ki =0. > Из условий (1.16), используя выражения (1.15), записываем <>~a(RL+M+aR~DR)~ а(1-2VBcos Xft + S) д.. (aR - D)Ko al - 2]/ cos U) 1 -aRKo aVВ sin U - cos U+/~ej (1.17) При совместном выполнении указанных условий имеем 4f(yh)=v(vh*) = [l; 1; 0; 0]; «а (vft+) = а/а; v = 2. 3, 4,... Таким образом, передаточную функцию цифрового регулятора можно записать в виде КоЩт+КгЩФ)г- + -{г- + г-+г-+.--) = 0 (, г-1)(1+о,г-1) • <-> где «2 (0+) = 1; = (ft+) = 1 - aRKo = /в i-sinU -cosUJ + e i-zVBcosKh + B • 6i = ;/.r)-«.(on = : a/? - £)- 1 = 2/Bcos XA; 6, = -i-- KoLm - aR-{-D = B. ±-КгиЮ a/Co Оптимальный цифровой регулятор при единичном ступенча-том воздействии на входе системы формирует следующие управляющие воздействия на входе объекта регулирования: гпо = (0+)= = Ко; «1 = «2 (ft-) = /Ci«2 {h*) = (1 - 2]/В cos %h) Ко; = = и {yh*) - а/а при V 2. Переходные процессы в интервале [0] [1] [2] [ 3 ] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] 0.0012 |