с периодом h в замкнутом контуре системы, что обеспечивается устройством синхронизации.

Рассмотрим временные процессы при отработке системой на рис. 2.1, а произвольного входного воздействия и (<). Эти процессы показаны на рие. 2.2. Входной сигнал и {() квантуется по времени идеальным квантователем (мгновенным ключом), который замыкается и размыкается мгновенно через каждые Т секунд. На выходе такого квантователя образуются мгновенные импульсы (6 -функции), площади которых и* равны входному

Фиксатор иН) г-п Г . ["п

рщптор Фиксатор

ОВъшт

7=Л/Л шсатор

Цифродсй

регуптор фиксатор

Объект

M(z) -- H(s) - 6ls)

Рнс, 2.1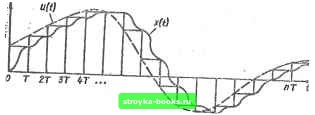

Рис. 2.2

сигналу в соответствующие моменты времени

«*=:«(/) при t = nT, л=0, 1, 2, ...

Фиксатор нулевого порядка преобразует последовательность мгновенных импульсов в последовательность прямоугольных импульсов длительностью Т, амплитуды которых равны входному сигналу н соответствующие моменты времени

Un-u{f) при t=nT, л = 0, 1, 2, ...

Система на рис. 2.1, а следующим образом отрабатывает последовательность сомкнутых между собой импульсов длительностью Т амплитудой Un= и (пТ): в . промежутке времени О <; < < У система отрабатывает ступенчатое входное воздействие величиной и (0), и в момент t == Т па ее выходе устанавливается величина х {Т) = и (0); н промежутке времени Т < t <: 2Т система отработает ступенчатое воздействие величиной

в (Т) = и{Т) - X {Т) = и (Г) - и (0), и в момент / = 22" на ее выходе устанавливается величина х (22") = и (Т); в промежутке времени 2Т < f<; система отработает ступенчатое воздействие величиной 0 (2Г) = « (2Г) - л: (27) = и (27) - и (Г), н в момент < = ЗТ на ее выходе устанавливается величина х (ЗТ) = и (2Т) и т. д. В промежутке времени пТ < t <. (п + I) Т система отрабатывает ступенчатое воздействие величиной 0 {пТ)= и (пТ) - - X (пТ) = и (пТ) - и[(п - 1) Т], и в момент времени 1= = (п + 1) У иа ее выходе устанавливается величина X [{п + 1) Т] = « (пТ).

Если задающее воздействие и (f) является гармоническим и (/) = t/„ax ®вх ™ максимальная ошибка при отработке системы задающего воздействия

Амплитуда и частота «=. 2/, задающего воздей-

ствия, а также максимальная ошибка 03 обычно заданы. Учитывая, что Т = Nh, где N - порядок линейного дифференциального уравнения объекта регулирования, находим условие, из которого можно определить шаг квантования /г, с которым работает оптимальный для ступенчатых воздействий цифровой регулятор:

При произвольном задающем воздействии u{f), которое изменяется с максимальной скоростью ю и максимальным ускорением egjj, для определения максимальной ошибки ©а удобно рассматривать эквивалентное гармоническое задающее воздействие Kj (t) = f jjjgjj g sin coj( с заданными максимальными скоростью и ускорением [12]:

= тах 9«вх. 9 = «тах = тах 9«вх. э =

Из последних двух равенств найдем параметры эквивалентного гармонического воздействия

W/«max; W.3 = ®max/ei

max-

Определим максимальную ошибку при отработке эквивалентного гармонического задающего воздействия

®гаах = fmax э «вх. 9 « тах э «вх. э-

Откуда

®тах 1 •гтахэ «bx.9

(2.2)

Определяя из условий (2.1) или (2.2) шаг квантования А, с которым работает оптимальный для ступенчатых воздействий цифровой регулятор н системе иа рис. 2.1, а, обеспечивают максимальную динамическую ошибку Б системе при отработке соответствующего задающего воздействия, не больше заданной.

Стремление уменьшить максимальную динамическую ошибку ©п,ая приводит к необходимости уменьшения шага квантования h, к увеличению общего коэффициента усиления разомкнутого контура системы /Са и как следствие к насыщению усилительного тракта. Система переходит в нелинейный режим. Можно найти минимальный шаг квантования h, при котором система еще будет работать в линейном режиме. Минимальному шагу квантования h соответствует ошибка

(®max)min == max в «ек. эКш- (2.3)

Структурную схему системы управления на рис. 2.1, а можно заменить эквивалентной структурной схемой на рис. 2.1, б, в которой оптимальный для ступенчатых воздействий цифровой регулятор описывается новой передаточной функцией М* (z)=M (z)/(l+z- + ...+г-Л+1), где М (z) - полином в числителе передаточной функции W (z). Цифровой регулятор е передаточной функцией М* (z) образует на входе объекта регулирования в эквивалентной системе на рис. 2.1, б точно такую же последовательное ь импульсов управления, как и цифровой регулятор с передаточной функцией W (z) в системе на рис. 2.1, а. Существенным я1вляется то, что в системе на рис.2.1, б входное воздействие и (t) может быть неэлектрнческой величиной, а элемент сравнения - преобразователем неэлектрической величины в электрическую (например, угла поворота в напряжение). Формулы (2.1) - (2.3) справедливы и для системы на рис. 2.1, б.

Рассмотрим пример. Пусть на вход системы на рис. 2.1, б поступает произвольное задающее воздействие, которое изменяется с максимальной скоростью w = 10° и максимальным ускорением еах ~ 5° с~. Тогда параметры эквивалентного гармонического воздействия

«вх. э = 8ах/«тах == так. в = ах/тах = 20".

Допустим, что динамическая ошибка слежения должна быть не более 0,5°, а объект регулирования описывается линейным дифференциальным уравнением второго порядка (N - 2). Тогда, согласно выражению (2.2), шаг квантования /г, с которым, работает оптимальный для ступенчатых воздействий цифровой регулятор, должен быть не более чем

, ®тах I „

А<р---д, = 0,025 с.

•тах э "вх. э* •

Пусть объект регулирования описывается передаточной функцией G (s) = а [s (s + b)]~, где частота сопряжения b - - 2 g"*. при h = 0,025 с необходимо обеспечить общий коэффициент усиления разомкнутого контура системы на рис. 2.1, 6, равный (см. табл. 1.1, п. 2),

°« = ft(l-%ft)°-

Итак, в системе на рис. 2.1, а (или и эквивалентной системе рис. 2.1, б), в отличие от системы на рис. 1.1, а, можно получить высокое качество при произвольных входных воздействиях и при