ва этих интервалах, что практически невозможно, так как прямая разность Ды„ при /< (n-f 1) Г неизнестна. Поэтому измеряют среднюю скорость на предыдущем, интервале

ulnT)~ul(n~l)T] = уг- =-у;- (г.ь)

и в результате экстраполирования получают

(О = «,»+ Оп-1 (< - «2"), • пГ < / < (и + 1) Г. (2.7) - как это показано на рис. 2.5.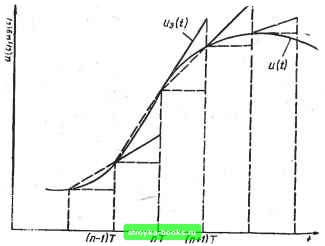

Рис. 2.5

Экстраполятор (фиксатор) первого порядка имеет передаточ-«ую функцию

1 j. 7*5 (1 - е-rs,» Т, (S) = -i*-- . (2.

Подставляя в уравнение (2.8) s = ja и Т = 2п/о)у, получаем частотную характеристику экстраполятора

1 -1- /глю/Юу 4 (sin лю/юу)2

Tj (/«) =

Фазовая и амплитудная частотные характеристики экстраполятора определяются выражениями [38]

2яю 2яю

ф (ю) = arctg -

ri(/co):

0+ о

43i2ffl2 XT / sin п«/юу \2

5 9-224

(2.9) 129

Рассмотрим систему на рис. 1.1, ос оптимальным цифровым регулятором для линейно-изменяющегося входного воздействия. Пусть система имеет объект регулирования е астатизмом 2-го порядка, динамика которого описывается линейным дифференциальным уравнением N-to порядка. Тогда при подаче иа. вход системы линейно-изменяющегося воздействия и {t) = U + at при t О к нулевых начальных условиях переходные процессы в сиетеме заканчиваются за время Т = Nh, и после окончания переходных процессов на входе последнего интегратора в схеме аналогового моделирования объекта регулирования устанав-

регдлятор

Фиксатор Объект -

ЦшрроШ

Фиксатор Сбьет

- His) - 6ls)

Рис. 2.6

ливается неличина, равная о, а на входах всех остальных интеграторов нулевые сигналы.

Предполояшм, что выходное воздействие и (f) является электрической неличиной (например, напряжением). Включим на вход системы дополнительно мгновенный ключ е периодом замыкания Т = Nh к фиксатор первого порядка g передаточной функцией Ti (s). Кроме того, будем измерять среднюю скорость входного воздействия измерителем скорости на каждом интервале (п - 1) Т < < <: пГ и на интервале пТ < < <i < (п + \) Т подавать эту скорость иа оптимальный для линейно-изменяющегося входного воздействия цифровой регулятор для перестройки его коэффициентов. Структурная схема системы управления для этого случая показана на рис. 2.6, а. Следует отметить, что выходной сигнал фиксатора первого порядка, включенного на входе системы, является линейной аппроксимацией непрерывного сигнала, и увеличение частоты квантования приводит к увеличению точности этой аппроксимации. Существенным условием правильной работы системы на рис. 2.6, а является синхронное и синфазное замыкания мгновенного ключа с периодом Т относительно мгновенного ключа с периодом Л в замкнутом контуре системы, что обеспечивается устройством синхронизации.

Рассмотрим временные процессы при отработке системой на рис. 2.6, а произвольного входного воздействия и (f). Эти процессы показаны на рис. 2.7. Пусть система в интервале

о <С i <i Т отрабатывает воздействие Оаб и одновременно измеряет скорость входного воздействия - наклон ае. Тогда в интервале Т <С t <:2Т система отрабатывает воздействие бег и измеряет скорость входного воздействия - наклон ед. После выхода в точку г система отрабатывает на интервале 2Т <z t <Z < ЗТ воздействие где и измеряет скорость входного воздействия - наклон 9э«. После выхода в точку е система отрабатывает иа интервале 37 < < <: 4Т скачок еж, наклон жв и измеряет скорость входного воздействия - наклон жи. Наконец,

ST t

Рис. 2.7

после выхода в точку в система отрабатывает на интервале 47" < < < <: 5Г воздействие вик и измеряет скорость входного воздействия ил и т. д.

На каждом интервале пГ < < « (и + 1) Г с выхода экстраполятора на вход элемента сравнения в системе на рис. 2.6, а поступает линейно-изменяющееся воздействие, скорость которого определяется средней скоростью а„ х на предыдущем интервале, и напряжение, пропорциональное скорости., подается на цифровой регулятор для настройки коэффициентов передаточной функции W (г). Таким образом, переходные процессы в замкнутом контуре системы на рис. 2.6, а на каждом интервале оптимальные и заканчиваются за время Т = Nh, После окончания пере-кодных процессов на интервале < < <! (и -Ь 1) 7" на входе последнего интегратора в схеме аналогового моделирования-объекта регулирования в момент t = (п + I) Т устанавливаете» величина, равная а„ i. Если скорость входного воздействия меняется от интервала "к интервалу (как показано на рис. 2.7), то. на каждом новом интервале для установки нового значения скорости добавляется соответствующее приращение скорости.

Таким образом, если скорость входного воздействия меняется от интервала к интервалу, то для перестройки коэффициентов цифрового регулятора подается напряжение, пропорциональное