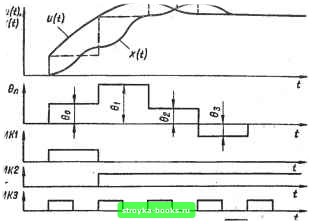Hand)

ивхг mod)

m(i)

jzm си I-I f

ri: J t

<6

<5

Рис, 2.11

о <: / < г на умножитель поступают сигнал ошибки 0оИ сигнал, равный расчетному коэффициенту Кр. На выходе умножителя формируется расчетный сигнал то = /Совд, который в промежутке О <: < < h поступает на вход объекта через ключ КлЗ. В промежутке h<.t<T блок на входе ключа Кл4 формирует сигнал то = (h)IKv - который поступает на вход объекта через ключ Кл4. В момент < = Г на входах 1 к 2 делителя формируются сигналы и кОдф) (эти сигналы обозначены на рис. 2.11 соответственно ui и kxs) которые сохраняются в интервале Г <: < < 27, и иа выходе делителя идентифицируется параметр Ко = (ft) i а на выходе умножителя

r2h Фчксотор "icfil

регилироНаиии

--Йдз-[

j д., fmcmncp Tzh

I

•Риксстор j2h

Рис. 2.12

формируется сигнал mot = ©i = • Этот сигнал поступает

на вход объекта через ключ КлЗ в промежутке Г <: i < Г + h, а в промежутке Г й < < < 27" блок на входе ключа Кл4 формирует сигнал tnix = Coi(Ji)IKv-ou который поступает на вход объекта через ключ Кл4 и т. д.

Нетрудно заметить, что передаточная функция блока, включенного перед ключом Кл4, равна идентифицированному пара-

метру - В. Действительно, Шщ == - Втоп = ~ - пцп Параметры /Со и в идентифицируются на каждом интервале. Если входной сигнал не изменяется и параметры объекта регулирования постоянны, ошибка в системе равна нулю.

Если изменяющимися или неточно рассчитанными параметрами в объекте являются постоянная времени Го = и коэффициент усиления Kv и есть возможность измерения скорости выходной Координаты объекта, то управляющие воздействия на объект регулирования, соответствующие реальным параметрам объекта, определяются по формулам (2.56) и (2.57). С учетом этих замечаний на основании этих формул можно записать

ftin = - Шоп

ОопФ/2)

fnon-i®n

где л - номер интервала регулирования (п = 0, 1,2,...).

Система с регулятором, реализующим эти вависимости, показана на рис. 2.12. Регулятор отличается от регуляторов в системах иа рис. 2.9 блоком (на рис. 2.12 обведен штриховой линией), который в соответствии с первой зависимостью формирует управляю1Щ1е воздействия в интервалах (« + h)T <: t < < (и -J- 1)Г, л = 0. 1. 2, ...

Этот блок состоит из двух умножителей, делителя, инвертора, вычитающего устройства, мгновенного ключа, моменты замыкания в котором смещены на время ft/2 относительно моментов замыкания мгновенного ключа в прямой цепи, и фиксатора. Нетрудно заметить, что передаточная функция блока равна идентифицированному параметру - В.

Таким образом, системы на рис. 2.9, б и 2.12 отличаются только блоками идентификации параметра й и работа этих систем иллюстрируется одними и теми же эпюрами (см. рис. 2.11).

2.3. УЧЕТ НАСЫЩЕНИЯ В СИСТЕМАХ УПРАВЛЕНИЯ С ЦИФРОВЫМИ РЕГУЛЯТОРАМИ

Нелинейность типа «насыщение» существенно влияет на переходные процессы в системах управления, значительно увеличивая время регулирования. Структурная схема системы с нелинейным элементом (ЯЗ) показана на рис. 2.13, а, характеристика нелинейного элемента с уровнем ограничения I/ -

Цифровой рееумтор

Фиттр ui(t)

ОНект

- H(s)

G(s)

m(i)

x(t)

Рис. 2.13

на рис. 2.13, б. объекта

При этом управляющее воздействие на входе

т(0 =

и2 (О при 1 И2 (О I « t/orp:

при 1 «L (О I > и,

огр»

где «2 (t) - управляющее воздействие на выходе цифрового регулятора (с учетом фиксатора нулевого порядка).

Для любого линейного объекта регулирования при ступенчатом входном воздействии величиной U можно определить шаг квантования Л, при котором система на рис. 2.13, а работает в линейном режиме, а регулятор обеспечивает оптимальные переходные процессы.

Пусть объект регулирования в системе на рис. 2.13, а описывается передаточной функцией G (s) " « Is (s + b)]-. Тогда для