получения оптимального переходного процесса при ступенчатом входном воздействии и нулевых начальных условиях цифровой регулятор должен иметь передаточную функцию (см. табл. 1.1, п. 2) с коэффициентом передачи Ко=Ь[ah(1 - e-bjj-i. При условии, что ир/Ко > и, система работает в линейном режиме и переходные процессы закончатся за время

Ti = Nh = 2h. (2.60)

Очевидно, минимальный шаг квантования й можно определить из трансцендентного уравнения

«« = Л(1-е-Ь*) =

(2.61)

Зависимости /Соа = 6 [ft (1 - е*"*)]-» при различных величинах b показаны на рис. 2.14. Определяя Ко из условия Ко = огр/»

произведению КвО. находим величину ft. При определенных отношениях forp/ полученный таким путем минимальный шаг квантования Л может не удовлетворять условиям (2.1) или (2.2). В таких случаях следует использовать цифровые регуляторы с неравномерным шагом квантования.

Если в рассмотренной системе цифровой регулятор с равномер-ным шагом квантования формирует управляющие воздействия то= = KoU в первом интервале длительностью ft и OTj = -еЬЬКи во втором интервале длительностью ft, то регулятор с неравномерным шагом квантования может формировать управляЮ1цив воздействия т = KU в первом интервале длительностью Ло и т = -Ки во втором интервале длительностью ftj. При этом переходные процессы заканчиваются за время

Tho+hi. (2.62)

Шаги квантования Лд и ftj связаны соотношением (1.148), а коэффициент передачи регулятора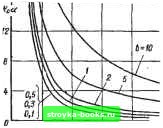

0,4 0,8

Рис, 2.14

1,г 1,6

- а М-

Aft = Ло - fh; fti = 7 In (2 - е-*)-Рассмотрим получаемое из формулы (2.64) выражение

6М = бЛо - 1п (2 - ё-"). Представим это выражение в виде

In e" = In е***» - In (2 - е>%

(2.63)

(2.64)

(2.65)

Обозначая е« = х и потенцируя левую и правую части уравнения (2.65), находим

2 - jt-i - 2jt - 1

= 0.

Таким образом, получаем квадратное уравнение относительно неизвестной величины х = е*». Корни этого уравнения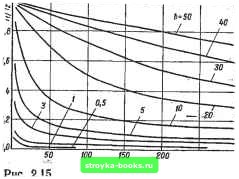

Единственное решение, соответствующее физической трактовке интервала h,

еЬК = gbAfi + YJKhJEh-C), (2.66)

Логарифмируя выражение (2,66), получаем

йй = т"И"+1--("-»)] • (2-67)

значению произве-

Определяя /С из условия /С дении /Са из формулы (2.63), находим

ДА = Ь/Ка. (2.68)

Далее по формулам (2.67), (2.64) и (2.62) последовательно определяем величины Ао. Ai и время регулирования Т. Выигрьпп в быстродействии, который обеспечивает регулятор с неравномерным шагом квантования по сравнению с регулятором, имеющим равномерный шаг h, при работе системы на рис. 2.13, а в линейном режиме при условии Кх, = К - VU можно оценить отношением TIT. На рис. 2.15 построены рассчитанные на ЭВМ по формулам (2.60)-(2.64), (2.67) и (2.68) графики зависимостей TjTi == f {Ко) при различных значениях частоты сопряжения b для системы рис. 2.13, а с объектом регулирования, имеющим передаточную функцию G (s) = a[s (s -j- Ь)]"*.

Еще больший выигрыш в быстродействии можно получить ДЛЯ систем упранления е объектами регулирования более высо-

кого порядка. Для регуляторов с неравномерным шагом целесообразно определять шагн квантования при одинаковой для каждого шага величине (амплитуде) управляющих воздействий на объект регулирования.

При поступлении единичного ступенчатого воздействия на вход системы на рис. 1.1, я, имеющей цифровой регулятор с не-равиомерньтм шагом и объект регулирования с передаточной функцией G (s) = cc/s*, по изложенной методике можно получить следующую систему уравнений для определения шагов квантова-вания (при нулевых начальных условиях и условии /«о j = j »2i = = \щ\ =m):

(hl~ti+hl)+- {hlhi + hl + hX-hX + hlh--tuhd+Khxh,

"2 "

\ К ~ ftf + fta) + Ml + hph - hih = 0;

fto - ftl + 2 = 0.

Решая эту систему уравнений, получаем

/!o = V2=ft2 = Ti/{4am). Переходные процессы заканчиваюгся за время

Га = + ftj + = 4йо = 2 Г Шат).

Для Данией системы с равномерным шагом квантования переходные процессы заканчиваются за время Г = 3ft н максимальнее управляющее воздействие »гах1 = li I = *iol == 2/(aft*).

Таким образом, Г = ЗА = 3 У2/(а ).

Определяя m и «1 из условия \ т\= \mi \ = VIV, находим выигрыш Б быстродействии, который обеспечивает регулятор с неравномерным шагом квантования по сравнению с регулятором, имеющим равномерный шаг, при работе системы на рис. 2.13, а в линейном режиме (когда объект регулирования описывается передаточной функцией G (s) = ct/s) Т. = 1,5.

В общем виде задачу синтеза оптимальных цифровых регуляторов в системе на рис. 2.13, а при наличии ограничения типа «насыщение» можно сформулировать следующим образом [28i. Для заданного входного воздействия типа и (г) = V или и (<)=" = и + at, заданной передаточной функции объекта регулирования G (s) и заданного вектора начальных условий х (0) необходимо определить параметры регулятора, при которых система управления вырабатывает заданное входное воздействие за минимальное число шагов квантования А и при этом амплитуды управляющих воздействий на входе объекта по абсолютной величине не превышают заданного уровня ограничения U{Ji>m. 2.13, б).

Для регулятора с неравномерным шагом квантования можно определить амплитуды ипульсов. оптимального управляющего воздействия на входе объекта регулирования при указанных входных воздействиях на входе системы управления. Амплитуды импульсов оптимального управляющего воздействия для статических объектов регулирования в системах, имеющих регулятор