Передаточная функция объекта регулирования

Амплитуды импульсов оптимального управляющего воздействия на входе объекта

obAB-F

/io + Ai + ft2 +

a + b ab

- an

CBqBi c(\-Bi)H Ъ

1- {l-B)F - A2{l-B2)FE\i

chpE-hxG + hFAB. M = - +

hjL - hiH + Б 5

. M,-6,)[ft,(l-Ba)-ft2Ba(i-Bi)l (l-B)E i

E = Л2В2 (В1-Л1) + Bj (i-Bj - (i-yy:

f = Л1В1 (B„-y,) + Bi (1-Bo) - (l~A„);

a = BiBa (1 - Л,) (1 ~ Bo) - AiA (1 --В)(1-Л);

H = BoflA (1 - 2) - Л1>12 (1 - Bt);

L = ЛВа [BoBi (1 - Л,) - Л„Л1 (1 - Bi)]; В„ = е-"°; Bt = e-\ Ве-

с неравномерным шагом, при единичном ступенчатом воздействии на входе систем приведены в табл. 2.1, а для астатических объектов регулирования при линейно изменяющемся воздействии на входе систем - в табл. 2.2.

Как видно из таблиц, амплитуды управляющих импульсов являются функциями параметров передаточной функции объекта и длительности шага регулирования 1ц, hi, hj, где N - порядок передаточной функции объекта регулирования, параметров входного воздействия и вектора х (0).

Пусть в цифровом регуляторе шаг квантования равен- ft. Тогда каждый шаг регулирования можно выразить в виде ftl = kh, где

Jt. -целое число, т. е hkoh; h\ = kih, .... ftJv»l = *лг-1-При этом ft!y>A.

Длительномь переходного процесса на выходе системы

V=0 V=0

где - целые числа.

Теперь задачу синтеза цифрового регулятора можно сформулировать так: необходимо определить числа k, при KOTopfclx Т = min и < Up {т - амплитуда на v-m шаге регулирования длительностью kji), и амплитуды импульсов управляющего воздействия на входе объекта регулирования при заданных передаточной функции объекта G (s) и входном воздействии и (/). Эта задача относится к задачам нелинейного целочисленного программирования с линейной целевой функцией и ограничениями в виде системы неравенств и не имеет универсального алгоритма решения. Рассмотрим алгоритм, основанный на мeтoe Гаусса - Зайделя, с использованием направленного перебора [29]. Аргументы k. функции Т \k), для которой необходимо найти минимум, ограничены снизу значениями kp = 1, й-[ = 1,

Схема алгоритма поиска оптимальных значений k, при которых Т == min и m., < i/pp, и расчета при определяемых шагах регулирования kh = амплитуд показана на рис. 2.16. Входными параметрами алгоритма (блок /) являются: шаг квантования А; число шагов квантования k*, которые укладываются в шаг регулирования при заданном уровне ограничения и прн равномерных шагах регулирования; заданный уровень ограничения foj-pl параметры входного воздействия и о; количество шагов регулирования TV, равное порядку передаточной функции объекта регулирования. В блоке 2 формируется массив ~ = k*, гдev==0,l.....N-l, т. е. начальное количество шагов квантования длительностью h в v-m шаге регулирования, а также рассчитывается начальное суммарное количество шагов квантования h по формуле ftj = Nk*.

Далее последовательно длительность каждого шага регулирования, начиная с N - 1-го, уменьшается на шаг квантования h (блоки 3 и 4). При этом каждый раз выполняется расчет амплитуд mi (1 = 0, 1, ... , N-l) на всех шагах регулирования hi = kih (блок 6) и сравнение полученных величин т/ с величиной огр (блоки 7-10). Если все значения < U, производится возврат к блоку 4. Если хотя бы одна величина mi превышает уровень ограничения Uorp управление передается блоку 12, где производится восстановление прежней величины k, (прибавление единицы к количеству шагов квантования на v-m шаге регулирования), и переход к (v - 1)-му шагу регулирования. В блоке 13 проверяется окончание цикла по количеству шагов регулирования. По окончании цикла оптимизации рассчитываетси суммарное ко-

личество шагов квантования h по формуле й = срав-

Q начат

h,k*U,d,N,Uoep 1-

г-г-

l(*l(**likz=kik=l<*

Расчет mi (L=0,U...,N-1}

kv-ki,*li v = v-/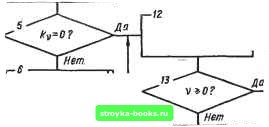

/(/ = 2 Лу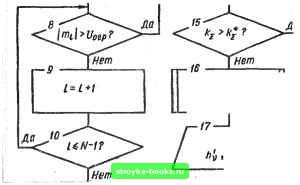

Расчет my

Вывод

Рис. 2.16