
 |
|
Главная Система автоматического управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [ 52 ] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] цивается й с (блоки 14 и 15). Если й < fej, то переходлт и блоку и для организации повторного цикла оптимизации. В качестве нового значения fej. принимается значение а fe* увеличивается на единицу и формируется массив k. Управление передается блоку S. Эта процедура вызвана тем, что оптимальнее значение может быть больше первоначального значения й*. а алгоритм производит только уменьшение й, начиная с = = k*. В случае равенства й и ftj; процесс оптимизации заканчивается, выполняется расчет амплитуд т. на полученных шагах 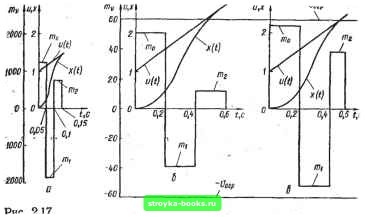 регулирования Н\ = kh (v = О, i,..., TV - 1) и вывод полученных результатов (блоки 16, 17). Блок 5 введен для устранения попытки уменьшения шага регулирования длительностью А(А== = I). Величину рассчитывают по, формулам или численными методами, и в схеме алгоритма этот блок выделен в виде подпрограммы. Рассмотрим следующую задачу. Система управления (рис. 2.13, а) имеет объект регулирования с передаточной функцией G (s) = » [s (s + а) (s + b)\, параметры которой равны а= 10 с~*, а = 5 сЧ Ь=2 с"*. Шаг квантования h равен 0,05 с. Нелинейная характеристика (рис. 2.13, б) имеет уровень ограничения U, равный 60. На вход системы поступает линейно-изменяющееся воздействие и {{) = U + ot, где U - 1; 0=3 с", при нулевых начальных условиях. Передаточную функцию W(z) цифрового регулятора е равномерным шагом регулирования определяем по табл. 1.4, п. 5. Если шаг регулирования принять равным шагу квантования ft, то получим следующие значения амплитуд упраиляющего воздействия на входе объекта (рис. 2.17, а): то = 1231,01; /«i =-19.30,05; = = 770,05. Эти значения намного превышают уровень ограничения t/rp. Если шаг регулирования увеличить до ft = ft*ft = = 4 . 0,05 = 0,2 е, то при расчете по тем же формулам получим следующие значения амплитуд управляющего воздействия на входе объекта (рис. 2.17, б): Ото = 51,1-3; 1Щ = -38,68; = = 12,06, где fe* - минимальное число шагов квантования (в каждом шаге регулирования ft), при котором амплитуды (V •»= О, 1, 2) еще не выходят ва уровень ограничения. Таким образом, используя цифровой регулятор о равномерным шагом то 50 iO 30 ZOIC -го- -(О -50 Ofti u(t] 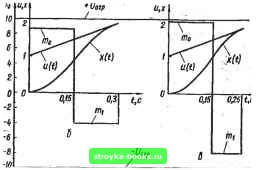 Рис. 2.18 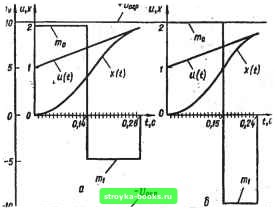 Рис. 2.19 регулирования К = k*h = 0,2 с, можно получить оптимальный переходный процесс в системе за время регулирования Т= Nh = 0,6 с. Рассмотрим регулятор с неравномерным шагом регулирования Ь = k,Jh. Амплитуды импульсов оптимального управляющего воздействия иа входе объекта определим по табл. 2.2, п. 5. Рассчитав по алгоритму (рис. 2.16), получим следующие значения (рис. 2.17. в): кц =4; ki= 4; feg =2; /По = 56,13; mi= ~ -52,43; «а = 38,59. taKHM образом, используя цифровой ре- гулятор с неравномерным шагом регулирования, можно организовать оптимальный переходный процесс в системе за время регулирования Г = fto + ftj + = (kp + ki + ft = 0,5 с. Пусть система управления (см. рис. 2.13, с) имеет объект регулирования с передаточной функцией C(s) = а, [s (s+ b)]~, параметры которой равны а = О с-2, Ь = 2 с-1. Шаг квантова- ния ft равен 0,05 с. Нелинейная характеристика (рис. 2.13, б) имеет уровень ограничения t/orp~ 0. На вход системы поступает воздействие и (Q = 1 + За при нулевых начальных условиях. Передаточную функцию W (г) цифрового регулятора с равномерным шагом определяем по табл. 1.4, п. 2. Если шаг регулирования равен шагу квантования ft, то амплитуды управляющего воздействия на входе объекта (рис. 2.18, а) равны: /Ло = 51,44; nil = -40,24, т. е. превышают уровень ограничения. Если шаг регулирования увеличить до ft = k*h = З- 0,05 = 0,15 с, то получим следующие значения амплитуд управляющего воздействия (рие. 2.18, б): = 8,56; Шу - -4,03. Оптимальный переходной процесс заканчивается за время Т - Nh = 2 • 0,15 = = 0,3 с. Используем регулятор с неравномерньш шагом регулирования h! = k. Выражения для амплитуд импульсов оптимального управляющего воздействия на входе объекта определяем по табл. 2.2, п. 2, Рассчитав по алгоритму (рие. 2.16), получим следующие значения (рис. 2.18, е): kp = 3; ki = 2; /и» = 9,69; nil ~ -8,03. Таким образом, оптимальный переходный процесс при наличии регулятора с неравномерным шагом заканчивается за время регулирования Г = fto + h - (ko + ki)h = 0,25 с. Если в системе управления используется меньший шаг квантования ft, то можно получить уменьшение времени переходного процесса не только в линейной системе управления без насыщения, но и в системе управления, имеющей нелинейность типа «насыщение». Пусть в рассмотренной системе с объектом регулирования второго порядка шаг квантования ft = 0,01 с, а остальные параметры прежние. Тогда при шаге регулирования, равном шагу квантования ft, амплитуды управляющего воздействия на входе объекта равны: = 1055,43; mj = -1004,23, т. е. намного превышают уровень ограничения. Если шаг регулирования увеличить до ft = k*h = 14 • 0,01 = 0,14 с, то получим следующие амплитуды управляющего воздействия (рис. 2.19, а): /Ио = 9,48; nil = -4,71. Оптимальный переходный процесс заканчивается за время Г = Ло • ft = 2 • 0,14 = 0,28 с. Используем регулятор с неравномерным шагом регулирования h - k,h. Рассчитав по алгоритму (рис. 2.16), получим . следующие значения (рис. 2.19, б). ko = 15; й] = 9; /По = 9,97; nil - -9,46. Оптимальный переходной процесс при наличии регулятора с неравномерным шагом заканчивается за время регулирования Т = h + ft, = (ko + j)ft = 0,24 с. Схема алгоритма расчета числа шагов квантования k*, которые укладываются в шаг регулирования ft = k*h при заданном уровне ограничения Чгр величин амплитуд управляющих воздействий, для регуляторов с равномерным шагом показана на рис. 2. 20. Входными параметрами алгоритма (блок /) являются: N - число шагов регулирования, равное порядку передаточной функции объекта регулирования; ft - шаг квантования; ир- заданный уровень ограничения; параметры входного воздействия I/ и о ы (О = U + at. Расчет начинается при 6 9-224 161 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [ 52 ] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] 0.0009 |