
 |
|
Главная Система автоматического управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [ 53 ] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] k = 1 (блок 2). В блоке S рассчитывают амплитуды {у - = О, I, N - 1), например, по формулам табл. 1.4. В блоках 4-7 выполняется сравнение величин m,, с уровнем ограничения t/ppp. Если хотя бы одна из величин превышает Г ввод lN,h,Uotp,V,6 п-з- Расчет тц г-«- к=к-и •огр» длительность шага регулирования увеличивается на шаг квантования h, т. е. k увеличивается на 1 (блок 9) и управление передается блоку 5. Если все \mi i/pp, управление передается блоку 8 (вывод величин h = и где v = 0,1, N- 1). Для получения оптимального переходного процесса в реальной системе, при отработке входного воздействия и (f) = = (7 + rt, поступающего на вход системы в момент времени / = О, необходимо найти длительности и амплитуды m., импульсов оптимального управляющего воздействия, соответствующие параметрам входного воздействия {U, а). Оптимальный переходный процесс можно получить только в том случае, если управляющее воздействие начинает поступать на вход объекта в момент времени t = О*, т. е. только в том случае, если задача определения оптимальных управляющих воздействий решается мгновенно. Однако реальные вычислительные устройства имеют ограниченное быстродействие и решение оптимизационной задачи можно получить только за некоторое конечное время Д/, а следовательно, и управляющее воздействие на объект регулирования можно подать только с задержкой ва время At относительно момента поступления входного воздействия. Наличие такой задержки приводит к тому, что переходный процесс в системе становится отличным от оптимального (рис. 2.21), Задержка выдачи управляющего воздействия приводит, во-первых, к увеличению длительности переходного процесса на величину Д, а во-вторых, к появлению ошибки Ах отработки за- 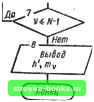 Рис. 2.20 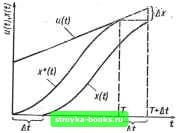 Рис. 2.21 данного входного воздействия, равной величине аД/. Таким образом, в реальной системе в общем случае можно получить только квазиоптпмальныи переходный процесс, степень близости которого к оптимальному определяется временем, необходимым для решения оптимизационной задачи. Рассмотрим некоторые способы построения оптимальных дискретных регуляторов и алгоритмы их функционирования, которые позволяют значительно уменьшить время Д< за счет решения оптимизационной задачи не в процессе функционирования регулятора, а на этапе его проектирования. Пусть имеем систему управления, в которой объект регулирования описывается передаточной функцией G (s) = а [s (s + b)]~ и имеет уровень ограничения по входу U. На вход системы поступает ступенчатое воздействие и (f) - U при < > 0. Необходимо построить дискретный регулятор, который обеспечивает оптимальные переходные процессы на выходе системы при заданной величине входного воздействия U = U,- Запишем выражения для амплитуд оптимальных управляющих воздействий на входе объекта регулирования при ненулевой начальной скорости объекта (см. табл. 1.8, п. 2) в виде mi=-Ko (Up-SpCo), J • b 1 hB f,u ™ o = ah(l~By > = У-Г=В: fie-*; /Co = bB hB ~ah(\-B) b ~ \ ~B- Амплитуды управляющих воздействий не будут превышать t/(,j,p, если выполнить совместные условия Ко 2 ° (2.70) Поскольку левые и правые части записанных неравенств являются функциями аргумента ft, то используя эти неравенства, можно найти минимальный шаг квантования ft = fe*fto, где k* - целое число, при котором эти неравенства выполняются. Зададимся вначале значением ft = fto, где fto - основной (минимальный) шаг квантования, и найдем U = U/Ko и U" = = огр/о при этом шаге. Если Uo=m\t\(U, U")U, то на вход объекта регулирования подаем U. и находим время 0. в течение которого выходная координата достигает значения тах -о» из уравнения X Ю = t/„ax - = t/opp (Mo - 1 + е"*»). Далее определяем • Оо (4) = аотах = torp X (1 - е~*-°) 6* . 163 и проверяем условия (2.70). Если условия не выполняются, то задаемся значением h = 2fto и повторяем описанную процедуру. Если снова условия (2.70) не выполняются, то задаемся значением h = ЗАо и повторяем процедуру. И так до тех пор, пока не определим h = h = k*ho, при котором условия (2.70) начинают выполняться. Фиксируем величины t. Up и aomax-которые соответствуют началу выполнения условий и рассчитанному значению шага h. Для полученного шага вычисляем амплитуды /Ло и /Л], а также коэффициенты Ко, Ко, Sq и So, необходимые для построения регулятора. Схема алгоритма расчета дискретного регулятора показана на рис. 2.22. В блоке / вводят исходные данные: параметры объекта регулирования а, Ь, минимальный шаг квантования ho, максимальное ступенчатое входное воздействие U, U. В блоках 2 к S задается количество шагов квантования длительностью ho в шаге h и определяется величина h = khp. В блоке 4 рассчитываются параметры цифрового регулятора Ко> К, So, как функции аргумента h. Величина линейной зоны Uo определяется в блоке 5 и сравнивается с в блоке 6. Если Up > тах (регулятор работает в линейном режиме), величины 4 и Оц принимаются равными нулю (блок 7) и управление передается блоку 12, в котором для найденных значений Uo к Оо рассчитываются величины Шо и т. Если t/p < (регулятор работает в нели- нейном режиме), рассчитывается время разгона объекта (времени возрастания выходной координаты от значения д; (0) = О до х (to) = = t/„ax ~ о) при подаче на вход объекта управляющего воздействия и для to находится Од (to) = Орах (блок 8). В блоках 9 и проверяются условия (2.70). Если условия не выполняются, управление передается блоку 10, гр,е величина 1г увеличивается на 1, и далее блоку 5. При выполнении условий (2.70) управление передается блоку 12. Блок IS выводит рассчитанные параметры ft, Ко Ко, So, So, Ug, to, а, то, т. Условия (2.70) можно получить в результате следующих рассуждений. Если Ко> Ко>0 (Ко = ВКо) « So>So>0(So = == So + ftB), то при Со = О амплитуды управляюниих воздействий не превышают U, когда Uo < U/Ko- При Со = Оощах из условия I «о <: (/огр получаем - (/огр Со < (t/o - «оошах) огр/О- Подставляя в это неравенство Uo = огр/о. находим первое из условий (2.70). Чтобы гарантировать отсутствие перерегулирования в переходном процессе ка выходе объекта регулирования, величину «1 выбираем из условия -(огр или -огр/0 <-го + 5;тао„ах<0. Подставляя в это неравенство-(7о = (/огр/о> получаем - (1 - В) и,/Ко < SVomax < forp/o. откуда при Ooniajj>0 получаем второе условие (2.70). 164 • [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [ 53 ] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] 0.0011 |