
 |
|
Главная Система автоматического управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [ 55 ] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] шаг квантования в цифровом регуляторе h = k*ho= 0,16 с (к* = 8), амплитуды управляющих воздействий йа входе объекта Щ = -7,62 и mj = -2,21, время регулирования < = 4 + + 2/1 « 0,58 с. При t/jjjj = 3 время переключения tp = 0,198 с, ошибка при переключении Uo - 1,28, выходная скорость объекта при переключении Орд = 16,33 с-1, шаг квантования в цифровом регуляторе h = k*ho = 0,12 с (й* = 6), амплитуды управляющих воздействий на входе объекта = -9,39 и mj = -2,09 (рис. 2.24, б), время регулирования / = <о + 2/i » 0,44 с; Ана- Чта» 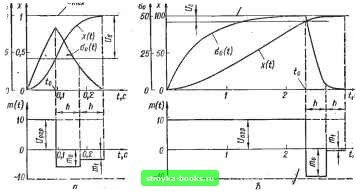 Рис. 2.25 логичным образом дискретный регулятор работает и при отрицательных скачках входного сигнала и (f). Дискретный регулятор, который рассчитан на скачок Uy, работает и при скачках U < U, обеспечивая меньшее время переключения to, но сохраняя расчетную величину ошибки при переключении Up и шаг квантования h в цифровом регуляторе, соответствующие величинеГ/а,;. Например, если на вход системы с дискретным регулятором» рассчитанным на величину скачка 5, подать скачок входного сигнала величиной U = Ъ то время переключевия to лирования to = to + 2/г 0,14 и /г = 0,16 с, т. е. время регу- 0,46 с, что немного больше, чем. в регуляторе, рассчитанном на скачок величиной U Чем больше величина скачка (/щах "Р" фиксированном U, тем больше время регулирования t = to-\-2h. С увеличением и x уменьшаются соотношения Uo/U и 2h/to. На рис. 2.25, а показаны переходные процессы в системе при (/„ах » времени переключения to - 0,096 с, величине ошибки при переключении Uo = 0,59, выходной скорости объекта при переключении Оцах = = 8,65 с", шаге квантования в цифровом регуляторе h = k*ho = ~ 0,08 с {к* = 4), амплитудах управляющих воздействий на входе объекта Шр = -5,93 и mj = - 3,45, время регулирования t - = + 2/г » 0,26 с. При [/„ах = (P"« 2-25, б) время пере- ключения to == 2,33 с, ошибка при переключении = 8,39, выходная скорость объекта при переключении Ооах = 9,53 (близка к предельной, равной Ua/b = 50 cl), шаг квантования в цифровом регуляторе h = k*ho = 0,34 с (k* = 17), амплитуды управляющих воздействий на входе объекта гпд = -9,17 и «1=-0,51, время регулирования /р =-f 2ft = 3,01 с. Таким образом, если при U = 1 отношения Up/U. и 2h/tp равны соответственно 0,59 и 1,67, то при U=100 эти соотношения равны 0,084 и 0,292. Если на вход системы поступает линейно изменяющееся воздействие и (О = тах + при О О, то амплитуды оптимальных управляющих воздействий на входе объекта регулирования при ненулевой начальной скорости объекта (см. табл. 1.8, п.2) Щ = -К (Uo + S[ai ~ Slap), j I h , 1ft где Si = 2ft + у - J д ; = 2ft + -J- - , a остальные коэффициенты определяются по формулам (2.69). Амплитуды управляющих воздействий не превышают U., если выполнить совместные условия i/„,p C„>Soaornax/2>0; - (1 - В) и,р/ко < s;ao„ax + hOi/B < U./Ko. (2.72) Условия (2.72) можно получить в результате следующих рассуждений. При 0(1 = 0 амплитуды управляющих воздействий не превышают U, когда Up <. и,.р1Ко~ SiOi- При ар - а из условия I /Пц I <: t/ppp определяем - ир/Ко < (Uo + SiOi - 5„а„„ах) < 1огр/Ко. Подставляя в это неравенство (/(, = [/p/ZCo - Sox, находим первое цз условий (2.72;. Чтобы гарантировать отсутствие перерегулирования в переходном процессе на выходе объекта регулирования, величину пгх выбираем из условия - U < <: О или - и/Ко< -Uo~ SxOx + S;ao,„ax < 0. Подставляя в это неравенство Up = U/Ko - Зх<Ух, находим - (1 - BWrp/Ko < (Si - Sx) Ox + SOpax UrpfKo, - откуда получаем второе из условий (2.72). Используя неравенства (2.72), можно найти минимальный шаг ft = k*ho, где й* - целое число, при котором эти неравенства выполняются. Зададимси вначале значением ft = fto, где fto - основной (минимальный) шаг квантования, и найдем UU/Ko-SxOx и U"Up/Ko~Sxai при этом шаге. Если U=mm(U, U")<cU, то на вход объекта регулирования подаем U и определяем время t в течение которого выходная координата достигает значения U -f- Oit - Ug, из уравнения * (о) = и т.. + 10 ~Uo= t/orp (Mo - 1 + Далее вычисляем <o(<o)=a„„,x = (/o,p.(l-e-S и проверяем условия (2.72). Если условия не выполняются, то задаемся значением h =.2Ао и повторяем описанную процедуру. Если снова условие (2.72) не выполняется, то задаемся значением ft == 3fto. И так до тех пор, пока не определим ft = ft = k*ho, при котором условия (2.72) начинают выполняться. Фиксируем величины 0. (/о и Сощах которые соответствуют началу выполнения условий и рассчитанному шагу ft. Для полученного шага вычисляем амплитуды гпр, rui, а также коэффициенты Ко, Ко, So, So, Si и S{, необходимые для построения регулятора. Структурная схема системы управления с оптимальным для входного воздействия и (t) = (7;, + Oit дискретным регулятором изображена на рис. 2.26. Эта схема отличается от схемы рис. 2.23, а дополнительным каналом, состоящим из измерителя скорости входного воздействия а, ключа Кл5,который замкнут при нулевом сигнале и разомкнут при ненулевом сигнале на его управляющем входе, мгновенного ключа с шагом квантования Т = 2Л и фиксатора нулевого порядка с передаточной функцией Г (S) = (1 - e-ys. При подаче на вход системы воздействия и {t) - U + aj при <>0 дискретный регулятор работает следующим образом. Если t/iax -- 0 ключи Кл1 - КлЗ разомкнуты и на вход объекта подается напряжение U до тех пор, пока выходная координата системы не достигнет величины U-\-ait - Uf,. При достижении выходной координатой указанного значения ошибка системы 0 (<) = =Uo, ключи Кл1-КлЗ замыкаются и на входы цифрового регулятора поступают скачок ошибки величиной Uo, скачок скорости входного воздействия величиной Oj (Q и скачок скорости изменения выходной координаты объекта величиной Оц (о) = Ошах-Цифровой регулятор формирует управляющие воздействия на входе объекта регулирования в соответствии с выражениями (2.71). Переходные процессы в системе на рис. 2.26 при параметрах объекта регулирования а = 10 с"*, ft = 2 с"*, U = 10 и основном (минимальном) шаге квантования в дискретном регуляторе fto = 0,02 с показаны на рис. 2.27 и 2.28.При и {{)-?, - - Ы (рис. 2.27, а) время переключения о » 0,12 с, ошибка при переключении Uo - 1,75, выходная скорость объекта при переключении o-Qjnax ~ 10,58 с", шаг квантования в цифровом регуляторе ft = *fto =0,12 с (k* = 6), амплитуды управляющих воздействий на входе объекта /Ид = -5,8; = -6,26. Время регулирования = 0 + 2А = 0,36 с. При и (О = 3 - 20/ (рис. 2.27, б) время переключения to « 0,015 с, ошибка при [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [ 55 ] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] 0.001 |