Рис. 2.26

±

T(s)

T[s)

ЧисрроВоШ рвеулктор

I Pukcamep

M(z)

H(s)

Объект регдтроВания

T(s)

•риштор j2h

6o(t)

Рис. 2.27

u(i)=3-m

переключении Uq = 2,69, выходная скорость объекта при переключении Oojg = 1,46 с-, шаг квантования в цифровом регуляторе h = k*ho=0,\4 с (fe* = 7), амплитуды управляющих воздействий на входе объекта Шо = -9,92; = -9,57. Время регулирования = t„ + 2h = 0,295 с. С увеличением отрицательной скорости входного воздействия время переключения tp стремится к нулю и дискретный регулятор работает как регулятор с равномерным шагом h, выбранным из условий /По 1 <: < forp и I mi К f/,

огр-

го 16

----10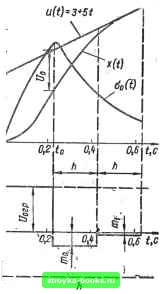

Рис. 2.28

При ы (if) = 3 -f 3< (рис. 2.28, a) время переключения /о«=0,225с, ошибка при переключении Uq f« 1,48, выходная скорость объекта при переключении Орд = 8Л2 С, шаг квантования в цифровом регуляторе А = fe*fto = 0,16 с (k* = 8), амплитуды управляющих воздействий на входе объаста /Пц = -5,88; mi = - 0,52. Бремя регулирования t = to-\-ih - 0,545 с.

При и (/) = 3 -f 5< (рис. 2.28, б) время переключения tp ~ f« 0,23 с, ошибка при переключении t/o - Ь83, выходная скорость объекта при переключении 0.= 18,6 с , шаг квантования в цифровом регуляторе h = k*ha = 0,2 с {k* = 10), амплитуды управляющих воздействий = -2,84; = 0,14. Время регулирования t= to + 2h= 0,63 с. С увеличением положительной скорости входного воздействия увеличивается время переключения to и шаг квантования в цифровом регуляторе h.

Рассмотрим систему управления (рис. 2.29,а), в кдаорой объект регулирования описывается передаточной "функцией C(s)s= а [s (s + 6)]- и имеет уровень ограничения по входу-

t/(jrp, a устройство сравнения имеет уровень ограничения по выходу в,р. На вход системы поступает ступенчатое входное воздействие и (/) = и при / > 0. Необходимо построить дискретный регулятор, который обеспечивает оптимальный(без перерегулирования, с минимальным временем регулирования) переходной процесс на выходе системы при заданном входном воздействии

Допустим, что устройство сравнения линейное. Тогда можно использовать дискретный регулятор, изображенный на рис. 2.23. При конкретных параметрах объекта регулирования и минимальном (основном) шаге квантования hp для этого регулятора можно

Устройство сравнения

Объект регулирования

mit)

mit)

Рис. 2.29

построить зависимости времени регулирования /р, ошибки при переключении Uq и выходной скорости объекта при переключении отах ™ скачка входного воздействия U. Эти зависимости при параметрах объекта и = 10 с~, 6=2 с~, U = 10 и шаге fto = 0,01 с рассчитаны по алгоритму на рис. 2.22 и построены на рис. 2.30, а. Предельная скорость об-ьекта определяется как Опред = огр "Z*- Предельной скорости q соо.тветствует предельная ошибка при переключении Uq . В свою очередь, величинам Cq рд и Uq соответствует определенное (максимальное) значение шага квантования ft* в цифровом регуляторе. Учитывая, что

. iorp/o {h*) = t/o = Л* (1 - е-"*) Оо пред. (2-73)

из условий (2.70) при = „рд находим следующее транс-

цендентное неравенство для определения ft*:

[So (ft*)

h* (1 g-*) > max

So (ft*)

(2.74)

(если величину ft вычислять не как дискретную feft„, k - целое число, а как непрерывную, то неравенство преобразуется в равенство). Значение Uq для рассчитанного ft* можно определить из выражения (2.73), при этом значение Uq для дискретного