аргумента ft* = ftfto превышает значение t/p, рассчитанное для

непрерывного аргумента ft* (с уменьшением минимального (основного) шага fto это различие становится незначительным). Из неравенства (2.74) видно, что шаг квантования ft* зависит только от постоянной времени объекта регулирования (частоты сопряжения Ь).

Для указанных параметров объекта и непрерывного мента ft получаем следующие значения: ft* я:; 0,328 с; Uq

пред

аргу-7,92

= 50 с-1. При ftfl = 0,01 с получаем ft* = 0,33 с к Uq

л! 7.97. При Ао = 0,02 с получаем А* = 0,31 с и [/д лг 8,39.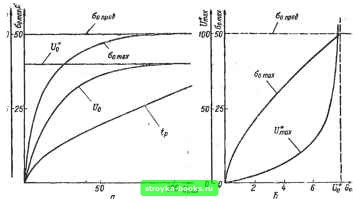

Рис. 2.30

Рассмотрим систему рис. 2.29, а с нелинейным устройством сравнения (рис. 2.29, б). Если Gp > to • ™ можно использовать дискретный регулятор, изображенный на рис. 2.23, и выполнить расчет этого регулятора по алгоритму на рис. 2.22. Если <:

t/p, то для заданного Qp выбираем ближайшее (насколько

позволяет минимальный (основной) шаг Ао) значение < ©огр условия

: ©огр. (2.75)

1У0--г-

Выбранному таким образом значению Up соответствует определенный шаг А, для которого по формуле (2.69) можно рассчитать параметры Ко. Кр, Sp и S;, для цифрового регулятора.

Для полученных значений Up к h согласно неравенствам (2.70) находим

aomax = "i"[2fo/5o; Up/Sh] (2.76)

и время Q, необходимое для нарастания скорости до этого значения, из уравнения . .

(2.77)

Выбранному значению Uf, соответствует не только определенная скорость Оо ах> "О и определенное значение U = V (рис. 2.30, а), которое можно найти из выражения

= + Оо щ>ед I (< - 1 + е-о). (2.78)

вагрУо= 7.92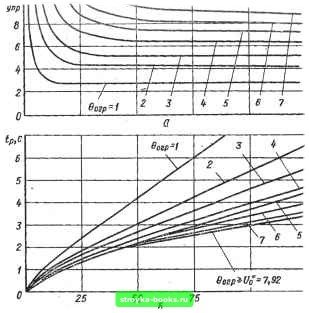

Рис. 2.31

Рассчитанные по выражениям (2.75)-(2.78) при указанных параметрах объекта регулирования зависимости Gqk U от 0огр построены на рис. 2.30, б.

Если полученное значение Uбольше или равно заданному входному воздействию U, то можно использовать дискретный регулятор, изображенный на рис. 2.23, и выполнить расчет этого регулятора по алгоритму на рис. 2.22 на заданное входное воздействие U. Если же полученное значение U меньше заданного входного воздействия U, то вместо управляющего воздействия t/ppp, подаваемого на вход объекта регулирования в течение времени t*, необходимо подавать на вход объекта новое управляющее воздействие Uy < U в течение другого времени tp. Два новых неизвестных t/p и t,, можно вычислить в ре-

зультате решения системы уравнений:

Oomax -

fmax-fo = %(W„-l+e-««).

(2.79)

Устройстбо

сравнений Цифровой

I----;---р eft) 7-2Л fUKcamp f, регуттр Фиксатор

Объект регулировании

Фиксатор -р,/.

T(s)

6o(t)

Рис. 2.32

В этой системе уравнений величины Ор, " рассчитаны ранее по выражениям (2.75) и (2.76), а f/j, ~ ""ое воздействие на входе системы. Время отработки входного воздействия величиной t/n,ax определяется как =to +2ft, где шаг h в цифровом регуляторе соответствует Uq.

Зависимости Uy и от величины U при различных Gp

и заданных параметрах объекта регулирования построены на рис. 2.31, а, б (при этом каждой кривой на рисунках соответствует определенное значение Uq и шага Л).

Хотя расчет дискретного регулятора для системы рис.2.29, а с устройством сравнения, имеющим нелинейность типа «насыщение» (рис. 2.29, б), и объектом, имеющим нелинейность типа «насыщение» (рис. 2.29, е), значительно сложнее по сравнению с расчетом дискретного регулятора для этой системы, имеющей только одну нелинейность в объекте, схема регулятора (рис. 2.32) аналогична схеме регулятора, изображенного на рис. 2.23. Единственное отличие заключается в том, что нелинейный элемент НЭ в системе на рис. 2.32 имеет уровень ограничения не U,

а lynp < огр (рис. 2.32, б).