XA + b\l-ah~j~JB~(a + b)AB

(1 Л)(1-В)

Из полученных выражений видно, что коэффициенты передаточной функции цифрового регулятора можно определить непосредственно через параметры передаточной функции объекта и шаг квантования Л.

Оптимальный цифровой регулятор при единичном ступенчатом воздействии на входе системы формирует следующие управляющие воздействия на входе объекта регулирования: шд = Ы2 X X (0+) = Ко; «1 = И2 = 6,/Со; Щ = (2Л+) = ЬКо. Переходные процессы в интервале О* t h, t ~х, определяются вектором

"1

aL (т) Ко аР (г) Ко aQ {1) Ко 1

(1.24)

йМ(т)-а2В(г) abx~(a + b) +-

ibV+b (• - ()]} • Q () = i 11 - -6 W15

Л (T) = e-"; В (T) = e-*".

Переходные процессы в интервале h+ < i < 2h, О* <: т < A; / = т + A определяются вектором

аКо IL + РМ (т) + QP (т) - (Л + В) t (т)] ®(т)= аКо[РЛ (T) + QU7(i;)-M + B)P(T)] , (1.25)

аД-oIQB (т)-(Л + В)(2(т)] l~aLKo

(т) = II - Л (т)]: Г (т) = rziT -

« (т) =

Переходные процессы в интервале 2h* / < 3ft, О* т h» . = т + 2/г, определяются вектором

а/Со[ + МР + Рд-(Л+В) 1] + аД-„[(й7(3

- BP) м (т) - лдр (т) -ь Лб1, (т)]

«/Со [{WQ - BP) А (т) - AQW (г) + ЛВР (т)1 aKoA[BQ{x)~qB{x)]

(1.26)

Пусть объект регулирования имеет параметры а = 10 c", 6=2 е"" а = 20 е""*. Определим передаточную функцию опти«

мального цифрового регулятора при шаге квантования h == = 0,1 с по формулам (1.23)

1 - 0,95407г-1 + 0,1 ЮЗОг"» W (г) - 255,204 j о,73850г-1 -f 0,08832z-a •

Переходные процессы при единичном ступенчатом воздействии и нулевых начальных условиях в системе на рис. 1.1, а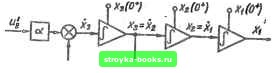

СЕН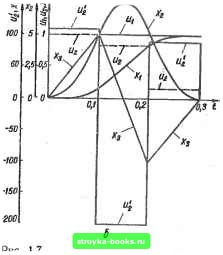

с указанным объектом регулирования и оптимальным цифровым регулятором, рассчитанные по формулам (1.24) - (1.26),: показаны на рис. 1.6, б.

Рассмотрим систему (см. рис. 1.1, а), в которой математическая модель объекта регулирования имеет два интегрирующих звена и описывается передаточной функцией G (s)=a [s (s+fc)]- Объект регулирования имеет астатизм 2-го порядка. Схема аналогового моделирования для такого объекта показана на рис. 1.7, а. Запишем дифференциальные уравнения состояния для системы на рис. 1.1, б с этим объектом регулирования (без учета переменного коэффициента усиления К): «i = 0; jf = х, х - х; х -

= - bxs; щ = 0. Уравнения переходных состояний такие же, как и для предыдущей системы. Переписывая уравнения в век-

1орни-«йтрачЮн юрмв V -= Av- и « (vA) = Bv (vA),,. по матрице А определяем дискретную Матрицу перехода Ф (А, /С) в виде [21]

Ф (ft. К) =

г 1 О О 0 0

о 1 А р. aLK О О 1 Q аР/С О О О В aQ/<- L О О О О 1

1 1ьч \

L[-2--bh + l~BJ,

(1.27)

а остальные коэффициенты определяются по формулам (1.3). Далее последовательно вычисляем

(0) = (Bv (0))» = [ 1; 0; 0; 0; 1];

даТ(Л) = (Ф(А, Ло)Ф(0+))=»[1: aLKo; аРКо; aQKo; U; T(h) = (Bv(h))r=ll; aLKo; аРКа, оДКа, X-aLKoYi ®(2А) = Ф(Л, /Ci)«(A+) = 1

а/Со (L + АР -f PQ) + ctL (1 - aZ,/Co) /Ci «0 iP + Q") + (1 - ai/Cc) /С, aBQ/Co + aQ (1 - a/Coi) /Cj . . 1-aL/Co

e (2/1+) = Bv ,(2A) i

a/Co (i + AP + PQ) + aL (1 - aLATo) /Ci a/Co (/ + Q) + (1 «i/Co) /Cj aBQ/Co+aQ(l -a/CoL)/Ci

F •• • , •

о(ЗА)=Ф(А. /Ca)o(2A+) = 1

a/Co {L+hP PQ) + aL (1 - aL/Co) Ci + aA [/Co (P +

+ Q) + P(l r- aLKo) Ki] + aP [BQKo+Q (1 -- aL/Co)/CiJ + aLF/Ca;

«/<o (P + Q") + aP (1 - aL/Co) + «Q [Q/o + Q(l-

-aL/Co)/Ci] + «P Ca:

aBQKo + aBQ (1 - aL/Co) + «QP/Ca.

"где F = 1 a [/Co (L + /iP + PQ) + L (1 - a/CoL) Ki].

Решая составленную на основании трех условий (ЗЛ) = Ij jtj (ЗА) = 0; лгз (ЗА) = О систему трех уравнений с тремя неизвест-ными, находим