Для рассматриваемой системы, используя подстановку г --H + w)l(l -w) п выражения (2.82) и (2.83), определяем

(2.85)

1-6, 1 -f В

{l~w}

(2.66).

w(l + BiW)

Типовые ш-передаточные функции цифровых регуляторов представлены в табл. 2.3, а ш-передаточные функции объектов регулирования (с учетом фиксатора нулевого порядка иа входе объекта) - в табл. 2.4.

Если для объекта регулирования, математическая модель которого описывается передаточной функцией <3 (s) = a[s (s + + 6)]-, ,параметры передаточной функции (2.82) цифрового регулятора рассчитаны точно, то ш-передаточиую функцию системы иа рис. 1.1, а в разомкнутом состоянии можно определить по формулам (2.84)-(2.86)

(1-ш)

2\ 1

w(l +Aiw)

Комплексная передаточная функция разомкнутой системы:

i+A

oi+fli 26

(l-jv)

iv{l+AiJv)

(2.87)

По функциям Kp(w)\ = /Cp(/j)) можно строить логарифмические частотные характеристики, т. е. зависимости амплитуды (в децибелах) и фазы (в градусах) от псевдочастоты. Непосредственно по этим кривым можно определять запасы по модулю и по фазе, характеризующие степень устойчивости системы, а перенося амплитудную и фазовую характеристики на обычную диаграмму замыкания, можно определять резонансный пик, резонансную частоту, полосу пропускания и оценивать динамические свойства замкнутой системы [33; 38].

При изменении псевдочастоты о от О до м действительная частота w увеличивается от О до ojft/2 = n/h. Перепишем функцию /Ср (Jv) в виде

/С„ (М = I /С (iv) I ехр {/ф„ (;)J ==B(v) + jM (V), (2.88)

\KpUv)[ = VB\v) + MHv); 4>o{v) = aTctglM(v)./B (v)\;

(2.89)

М {V) = -Ко pqrj 2 -

. (2.90)

Предположим, что параметры передаточной функции W {w) регулятора остались прежними, а параметры передаточной функции объекта изменились, и математическая модель объекта описывается передаточной функцией G (s) - а [s (s + b)]". Тогда ш-передаточная функция объекта регулирования имеет вид

rдeBl = L±; В-=,-№. 1 -В

В этом случае комплексная передаточная функция разомкнутой системы

26 jv(l+BM >

Kp(/i) = Ko 1 ,

.-(2.91)

Эту комплексную передаточную функцию можно представить также формулами (2.88) и (2.89), в которых

Kq/i 1 + fei (1 + ttf) (f) + (, - gi) Mq (ч) 2 1+a, \АУ

Kph l+bj (1 + AiBjV) Mg (V) -v(Ai- Bi) Bo (V)

M(v)

2 l+fli l + Av

., + 5,-(в,-Д)(,-В>)

B„ (t)

Mp {V) =

6 1 + Bt)2

. l-g,. + (e,-)(l+B,). 6 d (1 + bIv)

(2.92)

(2.93)

Таким образом, комплексную передаточную функцию в разомкнутом состоянии Кр(р) рассматриваемой системы на рис. 1.1, а можно определить по формулам (2.87)-(2.90), когда параметры оптимального цифрового регулятора точно соответствуют параметрам объекта регулирования, и по формулам (2.88)

(2.89), (2,91)-(2.93), когда параметры цифрового регулятора не соответствуют параметрам объекта регулирования.

В качестве примера рассмотрим систему на рис. 1.1, а, в которой шаг квантования ft = 0,1 с и объект регулирования имеет передаточную функцию G (s) = o[s (s-f 6)]"" с расчетными параметрами а = 10 с , 6 = 2 с Оптимальный для ступенчатых воздействий цифровой регулятор при таких параметра» объекта имеет передаточную функцию

1+Ь.г~ 1 -0,81872""

. () = oTT=""33j-q:o»-

Рассчитанные по формулам (2.88)-(2.90) логарифмическая амплитудно-частотная Kp(jv) и фазочастотная фр (v) характеристики показаны на рис. 2.36, кривые 1. По этим характеристикам находим: псевдочаетоту ереза = 0,356, запас устойчивости по фазе на этой-частоте v = 64°, запас устойчивости по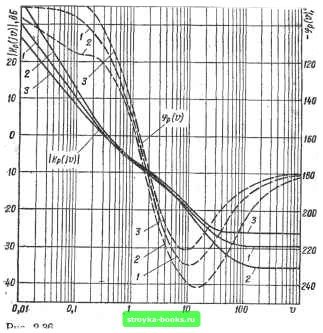

амплитуде 9,74 дБ (на псевдочастдте перехода фазовой характеристики через - 180°).

Изменим частоту сопряжения в объекте, например 6=1, оставив без изменения все остальные параметры системы. Рассчитанные по формулам (2.89), (2.92), (2.93) характеристики I Kpijv) I и фр(г) показаны на рис. 2.36, кривые 2. По этим характеристикам находим: псевдочастоту среза у. = 0,368, запас