теристикам находим: псевдочастоту ереза = 0,518, запас устойчивости по фазе = 71,14°, запае устойчивости по амплитуде 6,14 дБ.

Таким образом, изменение частота сопряжения Ь (постоян-времени Tj = 6 на гь50 % приводит к изменению псевдо-

частоты среза примерно на JQgg %. запаса устойчивости по фазе иа %, запаса устойчивости по амплитуде на q%.

5 *0

0,01 0,1

Рис. 2.38

Следует иметь в виду, что прн изменении частоты сопряжения Ь в передаточной функции объекта регулирования G (*) = = а [s(s-f-изменяется реальный коэффициент усиления объекта Kv = °-1Ь, а значит, и коэффициент усиления разомкнутого контура системы, что хорошо видно из графиков рис. 2.36 и 2.38. При произвольном (случайном) воздействии на входе систем управления определяют статистические характеристики воздействия (например, корреляционную функцию, спектральную плотность) и для этих характеристик находят такие параметры регулятора, при которых среднеквадратическая ошибка в системе минимальна.

HycTj корреляционная функция дискретного процесса на входе системы управления (рис. 2.37) имеет вид [13]

(2.97)

R (пТ) = De- " > cos Q пТ,

где D - дисперсия входного воздействия; Q - преобладающая частота в спектре входного воздействия; ц - коэффициент нере-1лярности.

Корреляционной функции соответствует спектральная плот -

2 шГ

ность в функции абсолютной псевдочастоты = 7 tg -g-

S(fo) =

(2.98)

где Si =

uT QT

1 + sh-sinY

shf + sinf uT QT

Использование абсолютной псевдочастоты tig = уг о (при этом Т

w = j-Vo) вместо псевдочастоты у удобно вследствие того, что

на малых частотах ft)(ft)<2/7) абсолютная псевдочастота практически совпадает с обычной, т. е. ti «(о, и частотные характеристики системы, построенные в функции псевдочастоты, практически совпадают с частотными характеристиками, построенными в функции обычной круговой частоты ш.

Дисперсию ошибки в системе управления с передаточной функцией Kpijvo) при случайном дискретном входном воздействии и помехе в виде дискретного белого шума с дисперсией Dg можно найти по формуле [13]

1 + К„ (Ро)

к„ in)

S{Vo)dvo

1 + /С„(Ю

(2.99)

Среднеквадратическая ошибка 6 = VDi.

Пусть ги-передаточная функция системы (рис. 2.37) в разомкнутом состоянии определяется выражением (2.94). Заменяя комплексную переменную w на jv, получаем комплексную передаточную функцию Kpijv)

(1 -/f) \mp + mi + jv

2(moB + mi) Ai («0+ mi)- th(l + B)

iv{l+ivAi)

(2.100)

-Используя выражение (2.100) и переходя к абсолютной псевдочастоте Do = Wflj , определяем комплексную передаточную

функцию системы в замкнутом состоянии и комплексную передаточную функцию системы по ошибке соответственно

/Сз(Ро)= i + K„uv„) -

/Се(/-о)=1+/с„(,Л) =

Со + Ро Jii + (/f)Pia

(2.101)

(2.102)

где Со = ah {Шр + mj); Ci = д g°a - Q = о - CgAi;

- Ohr.F & iu \ , r r 2« (mpB + /Яд) = 26+Ci; La = Л, (26 - Co) + io; -o =-b(l + B)

2.5. Л1инимальные дисперсии ошибки при различных частотах £2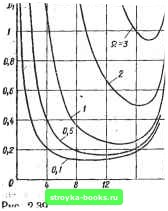

16 то

Подставляя выражения (2.101), (2.102) в формулу (2.99) и приводя интегралы в формуле (2.99) к табличным

П (Яо) rffp

0(ЫГ

(2.103)

где н (jv,y = б„ ФрУ"- + 6, ИщГ"- + • • • + fcn-i;

G (jvo) = а„ (/Ъ„)" + ai (/Ко)"" +•••+««.

вйределяем дисперсию ошибки при заданных характеристика» входного воздействия и. параметрах системы управления.

На рис. 2.39 построены рассчитанные по формулам (2.97)- <2.303) зависимости дисперсии ошибки Dj от коэффициента