дискретного регулятора (при условии, что = -Bwo), характеристиках входного воздействия D„ = 0,01; D = 3, р = 0.1, передаточной функции объекта регулирования G (s) »= 10 [s (s-f-+ 2)] 1, интервале дискретности Г = 0,2 с и различных преобладающих частотах Q в спектре входного воздействия. Для указанных на рисунке частот Q минимальные дисперсии ошибки Di и соответствующие этим дисперсиям коэффициенты и приведены в табл. 2.5.

2-5. СТРУКТУРНОЕ МОДЕЛИРОВАНИЕ СИСТЕМ УПРАВЛЕНИЯ КА МИКРО-ЭВМ

Для повышения качества и интенсификации проектирования систем управления, сокращения сроков и стоимости следует использовать средства вычислительной техники, разрабатывать новые ориентированные на ЭВМ методы и алгоритмы, предназначенные для моделирования и автоматизации проектирования современных САУ.

Среди различных методов моделирования САУ можно выделить два, основанных на использовании математических моделей , САУ в виде моделей состояния и структурных моделей. Однако моделирование САУ, представленных в виде моделей состояния, требует значительных объемов памяти и высокого быстродействия ЭВМ, что не позволяет реализовать этот способ на микро-ЭВМ.

Широко применяют структурно-топологические методы, по-вволяющие максимально использовать информацию о структуре исследуемой системы, где каждому типовому звену соответствует определенная модель. В основу алгоритма структурного моделирования типовых звеньев САУ положено использование единой модели универсального динамического звена. Задавая конкретные значения параметров моделей универсального динамического звена, можно получить различные типовые звенья. Поскольку при этом изменяются только исходные величины, то достигается высокая универсальность метода. При этом только вадание структуры исследуемой системы является нестандартным. Для этого все звенья системы нумеруют. Каждое звено имеет входной yi и выходной Xi сигналы {i ~ 1, 2, Л, где N - количество типовых звеньев в системе).

В состав модулей универсального динамического звена должны входить модели типовых линейных и нелинейных динамических звеньев. Конкретный набор моделей определяет поль-вователь в зависимости от решаемых задач. В табл. 1.3 записаны рекуррентные формулы, которые позволяют определять выход типовых линейных динамических звеньев как функцию их входа на данном шаге интегрирования, а также входа и выхода на предыдущем шаге интегрирования. При моделировании динамики САУ необходимо учитывать различные нелинейности. Рассмотрим алгоритмы моделирования некоторых типовых нелиней-ностей.

Схема алгоритма моделирования нелинейности типа «ломаная» и ее характеристика изображены на рис. 2.40, где XL{, YL{, /41 - абсцисса конца, ордината начала и коэффициент наклона i-ro участка соответственно. Данный алгоритм позволяет моделировать нелинейности типа «ломаная» с центрально-симметричным расположением участков относительно начала координат. Смещение характеристики относительно начала

координат легко реализуется путем соответственного смещения входной и выходной величин и выполняется в управляющей программе, определяющей структуру моделируемой системы.

Схема алгоритма моделирования нелинейности типа «реле с гистерезисом» и ее характеристика изображены на рис. 2.41,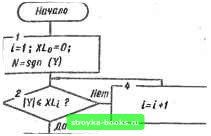

Конец

а

Рис. 2.40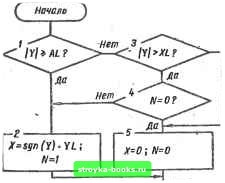

Конец J

XL AL У

Рис. 2.41

где AL, XL, YL - абсциссы включения и выключения реле и ордината выхода соответственно; N - идентификатор, характеризующий состояние реле в предыдущий момент времени (iV = О - реле выключено; N = I ~ реле включено).

Схема алгоритма моделирования нелинейности типа «гистерезис» и ее характеристика изображены на рис. 2.42, где XL, yL, AL - абсциссы нуля функции, перехода в насыщение, ордината насыщения соответственно; Л - идентификатор (N "= О - исходное (размагниченное) состояние; N = I - при уве-

личении входного сигнала, N ~ -I ~ при уменьшении); YI и XI - значения входа и выхода в предыдущий момент времени.

Схема алгоритма моделирования нелинейности типа «люфт» и ее характеристика изображены на рис. 2.43, где AL и XL -

Q Начало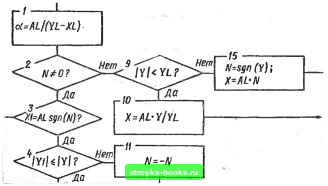

N=1? Лб Y<ZXL ? "нет

Нет 12-

У<-

г/3-

нет 16.

\~17

YiY/.-ZXL?~. Нет

X=AL

абсцисса нуля функции и коэффициент наклона; Y1 к Xi - значения входа и выхода в предыдущий момент времени. Для алгоритмов моделирования нелинейности N, Xi к YI ь начальный момент времени- равны нулю.

На основе полученных математических моделей можно построить подпрограмму моделирования универсального динамиче-