ского звена (рнс. 2.44). Входными параметрами подпрограммы являются: п - номер элемента в системе; - входная величина п-го элемента; hg - шаг интегрирования; Т - текущее время, а выходным параметром - - выходная величина я-го элемента. Подпрограмма содержит в себе подпрограммы низшего уровня: подпрограмму, начального диалога и подпрограммы моделирования типовых динамических звеньев.

уНтало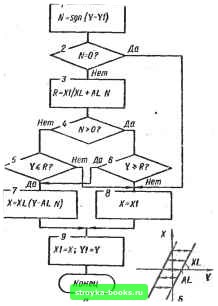

Рис. 2.43

Подпрограмма начального диалога (при я = 0) осуществля-ет ввод количества моделируемых динамических звеньев в системе, их типа и параметров в режиме диалога с пользователем. Введенный тип элемента и его параметры выводятся на терминал для контроля за правильностью ввода. В этой подпрограмме тип элемента привязывается к его номеру в системе и выполняется обнуление начальных условий. Введенные этой подпрограммой данные образуют рабочие массивы, с которыми оперируют остальные подпрограммы моделирования типовых динамических звеньев.

При обращении к подпрограмме моделирования универсального динамического звена с входным параметром пФ Q выбирается конкретная подпрограмма моделирования типового динамического звена, в которой К„ - идентификатор типа п-го элемента задается подпрограммой начального диалога.

Если идентификатор К„ не принадлежит к числу допустимых еначений, то выводится соответствующее сообщение и выполнение подпрограммы моделирования прекрашается. Подпрограммы моделирования типовых нелинейностей реализуют алгоритмы на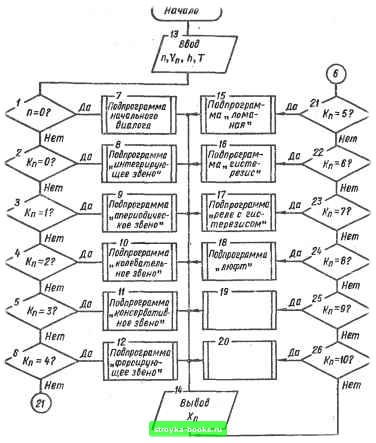

Рис. 2.44

Q Нонец

рис. 2.40-2.43. Набор подпрограмм моделирования типовых динамических звеньев можно значительно расширить. Например, можно ввести подпрограмму расчета рекурсивного Щ1фро-Бого фильтра по формуле

X (nh) = Ь{у [(« - О ft] - 5] «» X f(« -

1=0 j=l

где ft - шаг квантования цифрового фильтра (величина ft должва 202 "

быть кратна hg), а также подпрограмму звена типа «чистое запаздывание» и т. д.

При реализации алгоритма моделирования универсального динамического звепа необходимо, учитывать особенности алгоритмических языков, ориентированных для использования на конкретных микро-ЭВМ..

Глава 3 •

ЦИФРОВЫЕ РЕГУЛЯТОРЫ ДЛЯ СИСТЕМ УПРАВЛЕНИЯ ПРИ ПРОИЗВОЛЬНЫХ ВХОДНЫХ ВОЗДЕЙСТВИЯХ

3.1. ОСОБЕННОСТИ РЕАЛИЗАЦИИ ОПТИМАЛЬНЫХ ЦИФРОВЫХ РЕГУЛЯТОРОВ

При поступлении воздействия и {t) - U на вход системы управления (рис. 1.1, а), - имеющей статический объект регули-ронання, при поступлении воздействия и {() = t/ + of на вход системы (рие. 1.1, в), имеющей объект регулирования с астатизмом первого порядка, при поступлении воздействия и (Q =5 = t/ + о/ + на вход системы (рис. 1.1, г), имеющей объект регулирования с астатизмом второго порядка, и нулевых начальных условиях г-нзображеиие оптимального управляющего воздействия (при котором переходные процессы в системах заканчиваются за N шагов квантования длительностью h) на входе объекта регулирования имеет вид

М (г) = то+ mi г"! + mz-+ -. - + тг (1+г~ + z- + .. •)= 6„ + biz- + Ьг-М-" • +

где bg = /По; bx = mi - mg; ... ; bj - irij- Отдгр /га„ S

S m (vft"*") = «2 (vft*), a передаточная функция оптимального цифрового регулято"ра определяется в виде

+ biz- + -...+bz~ "-(1-г-)(У + «1г-М---+% 1г-+М

При поступлении воздействия и {{) - U на вход системы (рис. 1.1, а), имеющей астатический объект регулирования, при поступлении воздействия и (Q = t/ + of на вход системы (рис, 1.1, в), Имеющей объект регулирования с астатизмом второго или более высокого порядков, при поступлении воздействия и {t) - и at-\-Xt на вход системы (рис. 1.1, г), имеющей объект регулирования с астатизмом третьего или более высокого порядков, и нулевых начальных условиях г-изображение оптимального управляющего воздействия на входе объекта регулирования имеет вид

М (г) = /По + miz- + mz ------Ь тдг 1г-+ =

= &о + byz-i + 6,г-2 + ,.. + bi .z-"+\ (3,3)