
 |
|
Главная Система автоматического управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [ 67 ] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] где Ь(, = т,,; bi=m,; ... ; 6;v i =а передаточная функция оптимального цифрового регулятора определяется в виде Величины определяют площади мгновенных импульсов на выходе цифрового регулятора (амплитуды импульсов длительностью h на выходе фиксатора нулевого порядка) и зависят от параметров объекта регулирования, шага квантования Л и параметров входных воздействий U, а к %. Например, для объекта регулирования с передаточной функцией G (s) = a/s при линейно-квадратичном воздействии и (i) = U + ct + kt на входе системы оптимальный цифровой регулятор должен сформировать такое управляющее воздействие иа входе объекта регулирования, 2-изображение которого определяется М (2) = /По + miz- + тл,2-2 (1 -f z + z+...), US 2 „ и 1 гдеЛ? = 2; «о = + 2 о + - Я ; т--оа- - Я;тл, = -Я. При поступлении в момент 1=0 на вход системы управления (рис. 1.1, а, е или г) с оптимальным цифровым регулятором соответствующего типового воздействия ошибка системы при t Nh равна нулю, а на выходе регулятора в переходном режиме имеется последовательность из N импульсов т., = т (vh*), V = О, 1, N - 1. Переходный режим в системе заканчивается за интервал регулирования Т = Nh. Если при поступлении на вход системы (рис. 1. 1, г) произвольного входного воздействия измерять его величину, скорость и ускорение и в дискретные моменты времени / = пТ подавать на вход цифрового регулятора, оптимального для линейно-квадратичного входного воздействия, приращения Д« (nT"*") = = е (пТ+), До («r+) и ДЯ (пГ+), то регулятор на каждом интервале регулирования Т = Nh сформирует такие управляющие воздействия на объект регулирования, что система отработает указанные приращения на каждом интервале Т = Nh. Система управления (рис. 1.!, в) с цифровым регулятором, оптимальным для линfннo-изleняющeгocя входного воздействия, отработает на каждом интервале длительностью Т = Nh приращения Аи(пТ+) = в (пТ) и Да(пГ+). Система (рис. 1.1, а) с цифровым регулятором, оптимальным для ступенчатого входного воздействия, отработает на каждом интервале Т = Nh только ошибки в (пТ), т. е. приращения входного воздействия Д« (пТ*). Общая структурная схема системы, работающей при произвольных входных воздействиях, изображена на рис. 3.1. С выхода измерителя скорости и измерителя ускорения И; дискретные значения о («Г") и Я (пГ") поступают на звено задержки с передаточной функцией е" и вычитатель. На входы 2 и 5 цифрового регулятора поступают значения До (пТ) - о (пТ) - - € [(/г1)7-+ J и АЯ (иГ+) = Я (пТ*) - Я [(,г-1)Г+], п=0, h 2, ... . Дискретные значения ошибки 0 (п7") поступают на вход / регулятора. Общая структурная схема цифрового регулятора, построенная на линиях задержки ЛЗ, множительных устройствах и сумматоре, изображена на рис. 3.2. Количество элементов в схеме рис. 3.2 зависит, в первую ШпГ) очередь, от передаточной функции объекта регулирования. Например, при G (s) = a/s2 требуется уста- регулятор H(s) Gfs) x(t) Рис. 3.1. 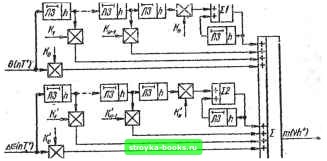 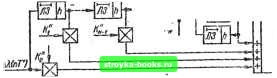 Рис. 3.2 повить следующие коэффициенты: Ко = / («А*); ki = =• -I/ {Лу.Ко = 3/(2a/i); К\ = -1/ (2a/i); Ко == 2/а; iCl" = = -2/а; Kii = К2 - 2/а, а также по одному элементу задержки в первых двух каналах обработки G (п7") и До (пГ*) и три элемента задержки в третьем канале обработки ДЯ {пТ*). Звенья е элементами задержки в обратной связи можно заменить дополнительными каналами формирования «подставок» (см. рис. 2.4, 2.8). На основе схемы рис. 3.2 можно построить большое количество схем цифровых регуляторов, которые обеспечат работу систем автоматического управления при произвольных входных воздействиях. При этом качество работы системы опре-деляется тем, какой оптимальный регулятор (оптимальный для ступенчатого, линейно-изменяющегося или линейно-квадратичного входного воздействия) положен в основу практической схемы цифрового регулятора, которая обеспечивает работу системы при произвольном входном воздействии. Регуляторы можно реализовать на аналоговых элементах [1; 2; 36; 43] и на цифровых элементах [2; 30; 35]. 3.2. РЕГУЛЯТОРЫ, ОПТИМАЛЬНЫЕ ПРИ СТУПЕНЧАТЫХ ВХОДНЫХ ВОЗДЕЙСТВИЯХ В общем виде контур систем автоматического управления с одним входом и одним выходом можно представить как последовательное соединение регулятора и объекта регулирования. При таком рассмотрении регулятор в системе рис. 3.1 представляет собой последовательное соединение мгновенного ключа с шагом квантования Т = Nh, цифрового регулятора с измерительными связями и фиксатора нулевого порядка G передаточной функцией Н (s) = = (1- e"fe)/s. Регулятор должен формировать требуемые управляющие воздействия на входе объекта регулирования. Техническая реализация регуляторов, оптимальных при ступенчатых входных воздействиях, на основе структурных схем рис. 3.1 и 3.2 (а также рис. 2.1, б и 2.4) будет различной в зави-
Рис. 3.3 ИУВХ 1Щ509 ТЬ. <Э1 CI 0,01 200и TR32.0 Н57ЧУД1 в., \Л5 -Ь -15в Рис. 3.4 еимости от того, какой объект регулирования (астатический или статический) имеется в системе. Наиболее простой задачей является построение регуляторов для систем с астатическими объектами регулирования Выходной сигнал таких регуляторов при ступенчатом воздействии на входе системы после окончания переходных процессов за время Т = Nh тождественно равен нулю. Функциональная схема регулятора, оптимального при ступенчатых входных воздействиях изображена на рис. 3.3. Схема [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [ 67 ] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] 0.0011 |
|||||||||||||||||||