(1 -ai/Ce) /Ci = -(1 + В) /Со: Л

(1+Д)/Со „ ВКо at/Co • «°°Т~ f = > - а (АР + PQ - Bi-) /С„.

о "Г a/i (Р - ер + Q2) •

• • • (1.28.)

Передаточную функцию цифрового регулятора определим по формуле (1.23), в которой с учетом выражений (1.3), (1.27) и (1.28) коэффициенты имеяют вид

о - ah (1 - В)

= «2(2/i+) = B; В = е-;

ах = "а-СА") == 1 - aL/Co

2 -6А

02 = «J2A+)=F =

26А (1 - В) •

1 -(бА+ 1 + -6=Aaj В (1 В) •

(1.29)

Оптимальный цифровой регулятор при единичном ступенчатом воздействии иа входе системы формирует следующие управляющие воздействия на входе объекта регулирования: т„ == Ы2 (О) =

= /Со; "i = "2 () = io; яа = И2 (2А+) = ЬКо Переходные процессы в интервале 0<:<<;А, t = T определяются вектором T(T) = [wi; xi; к; Xg-, щ]=11: аЦхЖь: аР (т)/С„;

где L(T) =

aQ(T)/Co: 1].

тЗ-бт-Ь 1-В(т) 1

(1.30)

-Ь в (т)]; Q (т) = -g- [1 - В (т)1; В (т) = е

Переходные процессы в интервале А*<<2А; 0*<!т<А; / = T-f-A, определяются вектором

а/Со [i + + <2Р () - (1 + В) L (т)1 да(т)= a/C„[P + (2Q(T)-(l-f В)Р(т)1 . (1.31)

a/Co[QB(T)-(l-bB)Q(T)] 1 - aLKo

Наконец, переходные процессы в интервале 21"* <; < < ЗА, 0*<т<А. t - X -\- 2h, определяются вектором

а/Со [hP + PQ-BL + x(Q-BP)~QP (,x)+BL (т)] V (т) = а/Со [Q -BP-QQ (т) -Ь BP (т)] a/Co[BQ(T)-QB(T)] l-a/Co(AP+PQ-Bi)

(1.32)

Пусть объект регулирования имеет параметры а = 10 с=; 6 = 2 с"*. Определим передаточную функцию оптимального цифрового регулятора при шаге квантования Л = 0,1 с по формулам (1.23), (1.29)

W [Z)- iw,M J o,82495z-i + 0,158392-2 •

Переходные процессы при единичном ступенчатом воздействии и нулевых начальных условиях в системе иа рис. 1.1, а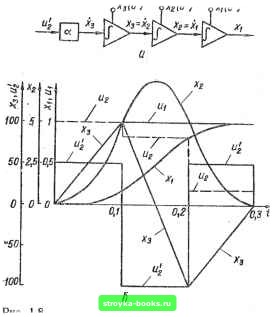

-с указанным объектом регулирования и оптимальным цифровым регулятором, рассчитанные по формулам (1.30) - (1.32), показаны на рис. 1.7, б.

Более просто можно определить передаточную функцию W (г) цифрового регулятора для системы на рис. 1.1, с, имеющей объект регулирования третьего порядка с передаточной функцией G (s) = a/s. Схема аналогового моделирования для такого объекта изображена на рис. 1.8, а. Запишем передаточную функцию цифрового регулятора по формуле (1.23), в ксггорой

Ко = 1/(аА«); Ki~ 12/5/Со; 2 = б/Со; «2 (О*) = 1:

= «а (/г+) = 1 -g- /Со = 5/6; = (2/г+) = 1 -

Ко+ahKo+(i - "Г f<c} т- 4

= «a(ft) = -2}

6a = ;«2(2ft*)=i.

Переходные процессы в интервале 0" < ? < Л, = т, определяются вектором

ф1(т) = [«1; xi, х; X,; и] = [\; тт); т=У(2/г*): т/А; 1].

Переходные процессы в интервале h*t<:2h, 0+<:т<:Л, t - X -\-h, определяются вектором

(т) = [1; 1/6 + т/(2А) + т=/(27г«) -xV{3h); 1/(2А) +

+ т/А2 т=/АЗ; 1/А= -2Т/ЛЗ; 5/6].

Переходные процессы в интервале 2А<:<<3/г, = т + 2А, 0*<:т<Л, определяются вектором

•»(T)=[1; 5/6-1-t/(2A)~t=/(2A) + tV(6/iS); l/(2ft)-т/А=+

+ T/(2ftS); -1/A2 + t/AS; 1/6].

ФггГо*; oXi(OV

о - о 0о

-гоо у00.

Рис. 1.9

Переходные процессы в системе (см. рис. 1.1, с) при ~ 20 с~*, h = 0,1 с изображены на рис. 1.8, б.

Рассмотрим систему (см. рис. 1.1, с), в которой математическая модель объекта регулирования описывается передаточной функцией С (s) = а [s (s -- 6s + а)\~. Схема аналогового моделирования для такого объекта изображена на рис. 1.9, о. Запишем дифференциальные уравнения состояния для системы на