
 |
|
Главная Система автоматического управления [0] [1] [2] [3] [4] [5] [6] [7] [ 8 ] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] вания показана на рис. 1.10, а. Оптимальная передаточная функция цифрового регулятора имеет вид К,и т + К (h) г + Кф., (2ft) г-g + Кщ (Ш) гЗ 1 (2) - «г (0+) + г-1 -I- «2 (2А+)г-= + «2(3/г+)г-8 = 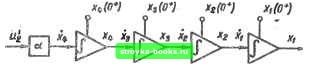 гооо -юоо -то 25 о .-50
3» Рис. 1.10 в которой /Со == 1/(а/г*); Ki-: /Са = 6/Со; /Сз = -24/Со: «а (О*) = 1; 01 = «2 (ft*) = 23/24; = (2/г+) = 1/2; = и, (ЗА-)= = 1/24. Оптимальный цифровой регулятор формирует следующие уп- Переходные процессы в интервале О* < < /г, / = т, определяются вектором да(т) = [«1, ха, хз, ;4. «J = [1; т*/(24й«); гЗ/(6й«); т2/(2А*): т/А 1]. Переходные процессы в интервале А* < / < 2А; 0+ т < А; < = С + А, определяются вектором ©(т) = 1/24 + т/(6А) + TV(4h2) + т8/(6А») - T«/(8ftS) 1/(6А) + x/(2h) + TV(2ft«) - т8/(2А*) l/(2ft)+T/ft8 -Зта/(2А*) 23/24 Переходные процессы в интервале 2/г+ < < ЗЛ, О* < т < Л, / = т-1-2А, определяются вектором Ф(т) = 1/2 + 2т/(ЗА) - т«/(ЗАЗ) + tV(8A*) 2/(3/1) -tW + t3/(2A*) - 2т/А» + Зт=/(2А4) -2/А8+.Зт/А* Переходные процессы в интервале ЗА+<:/<4А; 0+<:т<А; = T--3/i, определяются вектором 1»(т) = 23/24 + т/(6А) - т2/(4А=) + тЗ/(6АЗ) т«/(24А4) 1 /(6/1) - т/(2/1=) + tV(2A3) - т«/(6А*) -1/(2Л=)+т/А* -т7(2А*) l/ftS T/ft4 1/24 Переходные процессы системы (см. рис. 1.1, а) при « «= = 10 с"*, /г = 0,1 с изображены на рис. 1.10, 6. Синтез оптимальных цифровых регуляторов при входном воздействии типа ступенчатой функции для систем (см. рис. 1.1, а) с линейными объектами регулирования второго и третьего порядков и анализ переходных процессов при нулевых начальных условиях позволяют сделать следующие выводы. 1. Переходные процессы заканчиваются за два шага квантования мгновенного ключа (за время 2К) для систем с объектами регулирования второго порядка и за три шага квантования мгновенного ключа (за время З/г) для систем с объектами регулирования третьего порядка. 2. В момент окончания переходных процессов на входах всех интеграторов в схемах аналогового моделирования объектов регулирования устанавливаются нулевые сигналы. 3. Если объект регулирования имеет интегрирующее звено, после окончания переходных процессов установившаяся выходная величина цифрового регулятора равна нулю. Если объект регулирования не имеет интегрирующего звена, после окончания переходных процессов установившаяся выходная величина цифрового регулятора не равна нулю. 4. Передаточные функции W (г) оптимальных цифровых регуляторов для различных передаточных функции G (s) объектов регулирования второго и третьего порядков приведены в табл. 1.1 [19]. Коэффициенты передаточных функций цифровых регуляторов зависят от параметров объекта регулирования и шага квантования Л. Передаточные функции оптилтльных цифровых регуляторов для систем UI. л) при. ступеичапых входных воздействиях Передаточная функция объекта регу<ыропания 0(4) Передаточная функция оптимального цифрового регулятора W (г) 1 + Ьг- где Ко = l/(aft2); bi -1; fli = 1/2 s(s + 6) »l + 0i2-l где/Co bi = -B; 1-Д(1+М) «1= bh(\-B) (s + o) (s+6) i + M-" +V ""« 0 = а(1 Л)(1 - В) = fci = -(Л + В); 6g = ЛВ; fcB -сЛ-Кс -ЛВ «i-(fl-fc) (1-Л)(1-В)5 «0(1 г-1) (1 +«12-1)» «а где /Со = и(1 )г ; = -2Л5 Л(о/1-1+Л) «а + fcs + а при 4а -62>0 1.+ V-1 +у-2 Ao(j 2-i)(l+ai2-i) ™" > = «, 2/IcosM + B) • fej = -2 VB cos W; feg = B; Yb ( sin Ih - cos ?vft) + В "" 1 -2l/BcosU + B [0] [1] [2] [3] [4] [5] [6] [7] [ 8 ] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] 0.0011 |