
 |
|
Главная Интегральный монолит [0] [1] [ 2 ] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] областей полупроводникового материала, являются элементами III группы периодической системы элементов для областей р-типа и V группы для областей п-типа. Некоторые из легирующих примесей приведены в табл. 1-1. В производстве интегральных схем наиболее широко применяются бор, фосфор, мышьяк и сурьма. Тео}>ия диффузии Хотя процесс диффузии происходит в трехмерном пространстве одновременно во всех направлениях, для анализа основных его характеристик достаточно рассмотреть одномерную модель. Как будет показано в гл. 2, большинство полупроводниковых устройств, изготовляемых по планарной технологии, имеют такую форму и размеры, что применение для них одномерной модели является вполне оправданным. Основное свойство диффузионного процесса заключается в том, что частицы стремятся диффундировать из области с высокой концентрацией в область с низкой концентрацией со скоростью, пропорциональной градиенту концентраций между этими областями. Эта зависимость, известная как первый закон Фика, математически может быть выражена в виде где F - плотность потока частиц, т. е, количество частиц, проходящих через единицу площади поверхности, нормальной направлению движения в единицу времени; - концентрация, т. е. число частиц в единице объема; х - расстояние, измеряемое параллельно направлению движения частиц. Величина D называется коэффициентом диффузии и имеет размерность (длина)/время. Величина коэффициента D позволяет оценить относительную легкость или трудность движения диф- фундирующих частиц в данных условиях. Знак минус в формуле (1-1) показывает, что частицы движутся в направлении от области с высокой концентрацией к области с более низкой концентрацией. Во всех типовых задачах диффузии обычно интересуются изменениями концентрации примесей в зависимости от времени и расстояния. Фундаментальный закон диффузии, который связывает скорости изменения концентрации с пространственными координатами рассматриваемой области, можно вывести и:5 первого закона Фика, применяк ГШ шо ПВО 1WD won "с 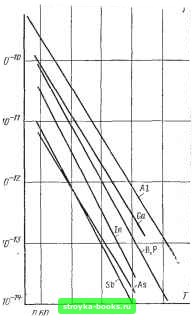 0,В5 DJD 0,75 1DD0/°£, Рис. 1-2. Зависимость коэффициента диффузии от температуры для различных jt-эге-рующих примесей. К нему принцип непрерывности. Рассмотрим область, или объем материала, ограниченную площадью А, нормальной направлению потока частиц и имеющей толщину dx. Поток частиц в этом объеме можно записать в виде dxA (1-2) и связать со скоростью изменения концентрации в. этом же объеме как dxA. (1-3) Выражение для дР/дх можно получить дифференцированием (1-1). Подставляя результат в (1-3),-будем иметь: (1-4) Это уравнение, известное как второй закон Фика, определяет распределение примеси в любой заданной точке полупроводникового кристалла в зависимости от времени. Коэффициент диффузии D является свойством конкретной легирующей примеси и представляет собой экспоненциальную функцию Бремени. На графиках рис. 1-2 приведены зависимости коэффициента диффузии различных примесей в кремнии от температуры. Так как выражение (1-4) является уравнением второго порядка с частными производными, его частное решение, пригодное для рассматриваемой задачи диффузии, зависит от граничных условий, которые связаны с конкретным процессом. Большинство диффузионных процессов, применяемых в произ- 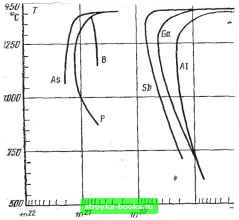 итомаВ/см Рис. 1-3. Зависимость предельной растворн-иости примесей в твердом кремнии от тем-I пературы. водстве интегральных схем, по граничным условиям можно отнести к одному из двух следующих типов: диффузия с постоянным источником и диффузия с ограниченным источником легирующей примеси. Далее рассмотрим отдельно характеристики диффузионных профилей, связанные с каждым из этих типов. Диффузия С постоянным источником При этом типе диффузии концентрация примесей у поверхности полупроводника поддерживается на постоянном уровне в течение всего цикла дифф5зии, т. е. N{0, /) = = const=Afci. Постоянный уровень концентрации примесей у поверхности полупроводниковой пластины определяется температурой и скоростью потока газа в диффузионной печи. В большинстве случаев при диффузии с постоянным источником можно полагать, что поверхностная концентрация Ло определяется предельной растворимостью конкретной примеси Б твердом кремнии. Как видно из рис. 1-3, предельная растворимость в твердом кремнии также сильно зависит от температуры. Процесс диффузии с постоянным источником описывается решением уравнения (1-4), удовлетворяющим граничным условиям N{0, f)=iVo-=const и N(x, t)=0. (1-5) Частное решение уравнения (1-4) можно выразить в виде N {X, f)==No(l~- J rtAJ, (1-6) где % - переменная интегрирования. Выражение внутри круглых скобок является хорошо известной и табулированной дополнительной функцией ошибок. Таким образом, концентрацию примеси в любой заданной точке кремния можно записать в виде Ar(x,/) = Ar„erfc(). (1-7) График дополнительной функции ошибок показан на рис. 1-4, а график распределения примесей, получаемый при диффузии с постоянным источником, показан на рис. 1-5. Заметим, что при таком типе диффузии полное количество примеси, диффундируемой в кремний, возрастает со временем. Иными словами, концентрация примеси в любой точке внутри полупроводникового материала (кроме поверхности) является монотонно возрастающей функцией времени. Следовательно, при /->10о вся вафля целиком будет иметь одинаковую концентрацию No. Если тип диффундируемой примеси отличается от типа проводимости материала подложки, то в точке, где концентрация диффундируемой примеси равна исходной концентрации, имеющейся в подложке, будет сформирован р-п переход. Глубина расположения переходов для различного профиля Рис. 1-4. Графики распределения примесей в кремнии при диффузии с постоянным (/) и с ограниченным источником (2). 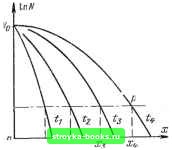 Исходная jfVHUBHm-<ация Рис. 1-5. Зависимость концентрации примесей от времени диффузии с постоянным источником. распределения примеси показана точками хи Х2 и лгз на рис. 1-5. При изготовлении монолитных интегральных схем диффузия с постоянным источником применяется на этапах изолирующей и эмиттерной диффузии. Пример. Необходимо сформировать р-п переход путем диффузии бора с постоянным источником в кремниевую подложку с начальной концентрацией примеск п-типа атомов в 1 см Диффузия выполняется при температуре 1250°С и npw поиерхностной концентрации бора, поддерживаемой на уровне его предельной растворимости в твердом кремнии. Определить время диффузии, необходимое для формирования р-п перехода на глубине 9 мкм. Решение. Поверхностная концентрация определяется из графика рис. 1-3 к равна iVo=5,5-10" атомов/см. При температуре 1250°С коэффициент диффузии бора равен 5-10-2 смс (см. рис. 1-2). Переход будет сформирован при условии, что N(x, t) будет равна исходной концентрации в кремниевой подложке, следовательно, 1.82-10-= erfc- где х=9 мкм. Решая относительно t я используя график рис. 1-4, находим -i =4000 с=66,5 мин. Диффузия с ограниченным источником легирующей примеси При этом типе диффузии полное количество атомов примеси, вводимое в полупроводник в течение всего процесса, является ограниченным. Это осуществляется путем предварительного нанесения на по- [0] [1] [ 2 ] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] 0.001 |