ГЛАВА ПЯТАЯ

ДИФФЕРЕНЦИАЛЬНЫЕ И ОПЕРАЦИОННЫЕ УСИЛИТЕЛИ

Дифференциальные усилители представляют широкий класс, схем, основным назначением которых является усиление разности между двумя сигналами. По этой причине их также иногда называют разностными усилителями. Уровни напряжения смещения и усилительные свойства дифференциального каскада в общем случае зависят от симметрии между двумя плечами схемы. Балансная природа дифференциального усилителя делает его идеальным усилительным устройством в интегральных схемах, так как монолитной технологии свойственно хорошее согласование элементов. Действительно, поскольку согласование номиналов и одинаковое изменение температурных свойств монолитных элементов значительно лучше, чем у аналогичных дискретных элементов, характеристики интегрального дифференциального усилительного каскада значительно превосходят характеристики обычного дифференциального усилителя в неинтегральном исполнении. Дифференциальный усилительный каскад используется в качестве.блока в схеме операционного усилителя. Поэтому монолитный операционный усилитель также обладает теми же преимуществами по сравнению с операционным усилителем на дискретных элементах.

В настоящее время наиболее широко распространенным классом аналоговых интегральных схем является монолитный операционный усилитель. В схеме такого усилителя можно достичь значительно более высокой степени сложности, чем в схеме операционного усилителя, выполненного на дискретных элементах! Так как все монолитные элементы изготовляются на пластинке одновременно, значительное повышение сложности схемы существенноулучшает ее характеристики без заметного увеличения стоимо-

сти. Таким образом, монолитный операционный усилитель почти всегда обладает значительными преимуществами в характеристиках и по стоимости, за исключением некоторых специальных устройств. В настоящее время стоимость монолитных операционных усилителей достигла столь низкого уровня, что они стали применяться в качестве простых элементов схемы в таких случаях, где еще несколько лет назад о их применении даже не помышляли.

5-1. ДИФФЕРЕНЦИАЛЬНЫЙ УСИЛИТЕЛЬНЫЙ КАСКАД

Дифференциальный усилительный каскад представляет собой балансную усилительную схему, предназначенную для усиления только разности между двумя входными сигналами. На рис. 5-1 показана принципиальная схема дифференциального усилительного каскада. Если предположить, что резисторы и транзисторы в обоих плечах схемы точно согласованы, то токи h и /2 в каждом плече схемы будут одинаковы при отсутствии входного на4 пряжения. Точно так же при этом и уровни постоянного выходного напряжения будут равны;

.Uor = V,,-.Ej-4. (5 1)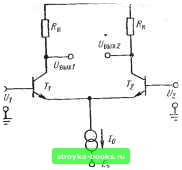

Рис. 5-1. Принципиальная схема дифферент-циального усилительного каскада.

Дифференциальный усилитель относится к классу схем, известных под названием симметричных. Поэтому для анализа характеристик схемы дифференциального усилителя при малых уровнях сигнала можно использовать хорошо известную из теории цепей теорему, называемую теоремой бисекции. Применение этой теоремы позволяет определить полностью все характеристики схемы путем исследования свойств только одной ее половины при данном фиксированном уровне входного сигнала, подаваемого на дифференциальный (несимметричный) или на обычный недифференциальный (симметричный) вход.

Симметричная схема может быть разделена на две части, каждая из которых является зеркальным отображением другой относительно оси симметрии. Символически это видно из рис. 5-2, на котором симметрич-ная схема N с двумя независимыми входами щ и «2 представлена в виде комбинации двух схем Ni и Лг относительно оси симметрии АА.

С помошью теоремы бисекции очень удобно анализировать симметричные схемы. Теорема устанавливает, что если схема может быть представлена в виде, показанном на рис. 5-2,6, и на ее симметричный вход подается сигнал «с, так что

«1 - «2 = Uc,

(5-2)

то токи и напряжения во всей схеме не перераспределяются при размыкании всех соединений между

Осб симметрии

-о-г-О-i

Рис. 5-2. Разделение симметричной схемы N на две схемы Ni и N2 относительно оси симметрии.

двумя частями схемы. Иными словами, все токи в соединительных ветвях от ii до in. между двумя частями схемы, обусловленные сигналом на симметричном входе, тождественно равны нулю. Аналогичным образом теорема бисекции устанавливает, что при подаче сигнала на несимметричный или дифференциальный вход схемы, когда имеет место равенство

Щ = -Ы2 = Uq,

(5-3)

токи и напряжения во всех внутренних соединениях между двумя частями схемы не изменяются, если эти соединения разомкнуть и соединить вместе в каждой из двух частей схемы Ni и N2. Или, иными словами, все относительные узловые напряжения ejh между /-м и k-ы узлами на рис. 5-2,6 при подаче сигнала"на дифференциальный вход тождественно равны нулю. Таким образом, при подаче сигнала на дифференциальный вход фактически имеет место как бы. заземление вдоль оси симметрии, так как ни одно из узловых напряжений по оси симметрии не подвержено влиянию входного сигнала с дифференциального входа.

Теорему бисекции нетрудно доказать, применяя метод линейной суперпозиции к токам и напряжениям в схеме, обусловленным подачей сигнала на каждый из независимых входов Ui и U2. Подробный анализ и доказательство этой теоремы здесь не приводятся, так как они хорошо изложены в известной литературе.

На рис. 5-3 представлена схема дифференциального усилителя в несколько видоизмененной форме с тем, чтобы ясно показать симметрию этой схемы. При подаче сигнала на обычный и дифференциальный вход схему рис. 5-3 можно анализировать путем разделения ее на две эквивалентные полусхемы относительно оси симметрии А-А в соответствии с теоремой бисекции. Режимы работы полусхемы при по-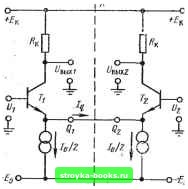

Рис. 5-3. Ось симметрии дифференциального усилительного каскада.

даче сигнала на симметричный вход и на дифференциальный вход показаны на рис. 5-4,а и б соответственно.

Если на симметричные входы Ui и U2 рис. 5-3 поданы одинаковые сигналы, т. е. Wj = «2 = «о, то и напряжения в каждой из симметричных полусхем будут изменяться одинаково. Относительный уровень напряжения с каждой стороны соединительной линии Qi-Q2 будет оставаться неизменным и ток /д в этой линии будет тождественно равен нулю. Таким образом, при условии, что сигнал подается на симметричный вход схемы, соединительная линия Qi - Q2 может оставаться разомкнутой, как это и следует из теоремы бисекции. Отсюда вытекает эквивалентная схема для случая подачи сигнала на симметричный вход усилителя, которая показана на рис. 5-4,а. Коэффициент усиления по напряжению дифференциального усилителя при подаче сигнала на симметричный вход очень невелик. Из эквивалентной схемы рис. 5-4,о коэффициент усиления по напряжению можно записать в виде

(5-4)

где St - крутизна транзистора Ti, определяемая как

5т = /o/2f/t, (5-5)

и Ro - внутреннее сопротивление источника тока Iq/2. Так как Ro ос, усиление каскада по напряжению при подаче сигнала на симметричный вход очень мало.

Если входной сигнал подать на дифференциальный вход каскада рис. 5-3 (т. е. Ui = -u2 = Uq), то ток и напряжения в каждой из симметричных полусхем будут изменяться в противофазе. При этом напряжение Uq на соединительной линии Qi - Q2 не будет изменяться и фактически эта линия будет как бы заземленной, как это и следовало из теоремы бисекции. Следовательно, при подаче сигнала на дифференциальный вход схему усилителя при малом сигнале можно анализировать, используя эквивалентную полусхему рис. 5-4,6. Коэффициент усиления схемы при этом равен коэффициенту усиления обычного каскада с общим эмиттером

Ки2=-RkSh- (5-6)

Как видно из равенств (5-4) и (5-6), усилительные характеристики дифференциального каскада существенно различны в случае подачи входного сигнала на дифференциальный и симметричный входы. Способность схемы усиливать сигналы, подаваемые на дифферец-циальный вход, и ослаблять сигналы, подаваемые на симметричный вход, известна как свойство ослаб-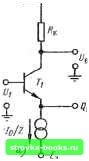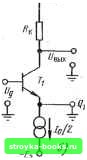

Рис. 5-4. Эквивалентные полусхемы дифференциального усилителя при подаче сигнала на обычный вход (а) и на дифференциальный, вход (б).