
 |
|
Главная Интегральный монолит [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [ 47 ] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] Рис. 7-2. Базовая схема дифференциального кас ада, используемого в качестве устройства умножения с переменной крутизной, умножителя с переменной крутизной легко понятен из рассмотрения дифференциального усилительного каскада на рис. 7-2. При небольших входных напряжениях Ui, удовлетворяющих условию Ui<Ui:, зависимость дифференциального выходного напряжения f/вых каскада от входного напряжения может быть представлена в виде t/Bbix = S,i?Hf/l, (7-6) где t/т - тепловой потенциал; St=UUt. (7-7) Крутизна каскада может изменяться при помощи второго напряжения U2, подводимого, как показано на рисунке. При этом если /ээбэ, напряжение с током /э связано следующим образом: (7-8) На основании (7-7) и (7-8) характеристика передачи по напряжению каскада запишется: t/вых := grRuU, = (U,U,) (7-9) т. е. в виде, аналогичном выражению (7-1). В простом умножителе с переменной крутизной суммарный эмиттерный ток /э изменяется в зависимости от управляющего напряже- ния Uz- Это обусловливает изменение в широком диапазоне напряжения общего типа, что нежелательно в случае, если требуется несимметричный выход или согласование по постоянному току. Значительное изменение напряжения общего вида может быть исключено путем использования параллельного включения двух дифференциальных каскадов и перекрестного соединения их выходов, как показано на рис. 7-3. Два входных напряжения Ui и Uz задают распределение суммарного тока /т между различными ветвями схемы. Однако, поскольку суммарный ток /т остается постоянным, а входящие в систему ветви соединены симметрично-перекрестно, существенного изменения напряжения общего вида на выходе не происходит. Поскольку схема умножителя, показанная яа рис. 7-3, значительно сложнее схемы рис. 7-2, использование в ней принципа переменной крутизны не столь очевидно. Оперируя распределением токов между ветвями, явление умножения сигналов, можно объяснить следующим образом. Допустим, что все элементы,, входящие в схему, хорошо согласованы и что для всех транзисторов 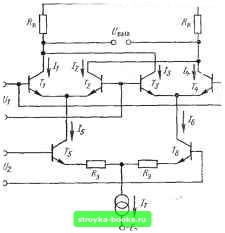 Рис. 7-3. Устройство умножения с переменной крутизной на основе спаренного дифференциального каскада с симметрично-перекрестными связями. РоЗ>1. Тогда для токов, протекающих в ветвях, справедливы соотношения: Л + /. = /5; /,4-Д=/е; и,и„ (7-18> (7-10) Принимая, что входное напряжение Ui достаточно мало, так что (/i<CC/t, разбаланс токов в дифференциальных каскадах (Ti, Тг) и {Ts, Ti) можно представить в виде {h~h) = {S)izUi (7-11) h-h=-{S)siUu (7-12) где (5т) 12 и (St) 34 - крутизна пар транзисторов {Ti, Tz) и (Гз, Г4) соответственно. Вследствие того, что в эмиттерных цепях дифференциальных каскадов отсутствуют резисторы, величины крутизны соответствующих транзисторов прямо пропорциональны токам смещения /5 и h: (5т),. = и (5,.)з4 = . (7-13) Суммарное выходное дифференциальное напряжение С/вых может быть представлено в виде (/вых = Rn [(/1 - h) -f (/3 - /.)]. (7-14) Тогда на основе выражений (7-11) - (7-13) выражение для выходного напряжения (7-14) может быть записано: (/вых = (/,/?н [(St).. - {Sr),4 = (7-15) Если резисторы Rs в эмиттерных цепях транзисторов Г5 и Ге выбраны достаточно большими, так что /5/?э»(/т и /б/?э»(/т, (7-16) то разность между токами /5 и /е пропорциональна Oz: (/.-/е) = Подставляя (7-17) в (7-15), получаем выражение (/иых= аналогичное выражению (7-9). На примере схем, изображенных, на рис. 7-2 и 7-3, показаны основные принципы построения умножителей с переменной крутизной. К сожалению, в случаях, требующих высокой линейности умножителей, динамический диапазон обеих этих схем. очень ограничен. Это объясняется тем, что выражения (7-9) и {7-18). справедливы только в ограниченном-диапазоне изменения (/i, а именно при I (/i I Ui. Таким образом, при условии обеспечения высокой линейности величина входного напряжения Ui должна быть ограничена несколькими милливольтами. Если величина на-пряжения Ui сравнима с величиной температурного потенциала Ui или -превосходит его, то пары транзисторов {Ti, Гз) и (Гг,, Г4) работают как синхронные ключи, которые замыкаются или размыкаются в зависимости от полярности-напряжения Ui. В этом случае-устройство работает уже не как умножитель, а как балансный модулятор. Использование названных схем для этой цели будет описано в последующих параграфах. 7-4. монолитный ЧЕТЫРЕХКВАДРАНТНЫЯ! УМНОЖИТЕЛЬ На пути расширения динамического диапазона умножителей, описанных в предыдущем параграфе,, имеется одна принципиальная трудность. Она заключается в том, что-в определенном диапазоне линейность умножения достигается за счет пропорциональности крутизны транзисторов Г1 и Tz на рис. 7-2 (или пар транзисторов Ti, Tz и Гз, Г4 иа рис. 7-3) их эмиттерным токам. Это справедливо только при малых входных сигналах (т. е. I (/i I <С (/т) и при условии отсутст-(7-17) ВИЯ снижения эффективности эмиттера. Из рассмотрения рис. 7-2 еле- .дует, что при большом входном сигнале переходная вольт-амперная характеристика дифференциального каскада на транзисторах и Гг становится нелинейной. При этом -зависимость коллекторных токов h -и /г от входного напряжения t/j описывается выражением (7-19) Для обеспечения линейности умножения в широком динамиче-ском диапазоне необходимо тем или :иным способом линеаризовать экс--поненциальную переходную вольт-амперную характеристику (7-19). Зто может быть достигнуто, напри-.мер, путем предварительного нелинейного преобразования входного напряжения t/j при условии высокой точности и хороших регулировочных свойствах нелинейного преобразователя. Например, предположим, что входное напряжение .подано на дифференциальную схему. Тогда фактическое дифференци-альное напряжение Uu подводимое к базам транзисторов и Гг, будет ЯВЛЯТЬСЯ логарифмической функцией входного напряжения Uu В ре--зультате чего экспоненциальное выражение (7-19) окажется линеаризованным. В этом заключается основной принцип построения интегральных полупроводниковых четы-рехквадрантных умножителей. На рис. 7-4 приведена упрощенная принципиальная схема устройства, обеспечивающего получение 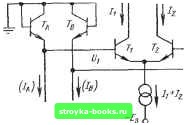 Рис. 7-4. Формирование логарифмической -функции от входного напряжения, подаваемого на вход дифференциального каскада. напряжения (f/i), пропорционального логарифму входного сигнала, с целью линеаризации переходной вольт-амперной характеристики дифференциального каскада с общим эмиттером. В этом случае для смещения транзисторов и Гг используются транзисторы Га и Тв, включенные по диодной схеме, как было описано в § 4-1. Включенные по диодной схеме транзисторы смещаются токами управляемых источников тока 1а и 1в- Величина напряжения сигнала Uu снимаемого с этой цепи, определяется разностью токов 1а Я 1в Я может быть представлена в виде U, = Urln (7-20) Подставляя (7-20) в (7-19), можно обнаружить, что токи дифференциального каскада h и /г пропорциональны токам смещения: f- (7-21) Причем на эту зависимость не влияет нелинейность входных характеристик транзисторов. Величины токов, протекающих в соответствующих ветвях схемы, с величиной общего тока смещения связаны следующим образом: (7-22) -. (7-23) Необходимо отметить, что при выводе выражений (7-20) - (7-23) не было принято никаких ограничений на максимальные величины токов схемы. Поэтому все названные выражения справедливы в широком диапазоне токов при условии, что характеристики элементов хорошо согласованы и падение напряжения на входе транзистора f/бэ описывается простым уравнением диода (2-1). Поскольку интегральным полупроводниковым схемам свойствен- [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [ 47 ] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] 0.0011 |