где интегрирование проводится только в пределах объема активного слоя Va-

Предполагая, что испускание в активном слое однородно, и вынося /?л/г1л в (2.19) за знак интеграла, имеем

Г1ЛГ1"

/?л.

(2.20)

Спектр люминесценции определяется энергетическим распределением инжектируемых в активный слой носителей. Это распределение задается квазиуровнями Ферми Fe для электронов и Fh для дырок и температурой диода Т. Для лазерных полупроводников таких, как GaAs, обычно hvkT, и, кроме того, вблизи порога, когда выполняется условие S.F=Fe - FhkT, скорость люминесценции практически совпадает со скоростью спонтанной рекомбинации .

/?с„= 5 /?c„(v)dv= JWc„(v)dv, (2.21)

где Wcn(v) - удельная мощность спонтанного излучения.

Вычисление порога генерации основано на совместном решении уравнения баланса, уравнения электронейтральности и энергетического условия генерации. При расчетах применяется следующий формальный прием. Задается значение уровня Ферми для электронов

и из уравнения нейтральности определяется уровень Ферми для дырок F. По известным F и f,, рассчитываются для заданной модели вещества коэффициент усиления и мощность люминесценции. Максимальное значение /Cyc(v) по условию равно коэффициенту потерь, а /п связано с /?л соотношением (2.20). Таким образом, устанавливается связь между /п и «„.

Зависимость порога от толщины активного слоя. В принципе зависимость порогового тока от толщины активного слоя может быть обусловлена тремя факторами. Во-первых, при заданном количестве носителей, инжектированных через р - п-переход или гетеропереход, их концентрация в активной области будет тем больше, чем меньше объем этой области. С увеличением толщины активного слоя уровень заполнения зон будет уменьшаться. Этот фактор учитывается формулой (2.20), согласно которой пороговый ток прямо пропорционален d. Во-вторых, если толщина активного слоя сравнима с длиной волны генерации К, то коэффициент потерь

будет функцией d, поскольку р зависит от d. В-третьих, уровень усиленной люминесценции в значительной степени определяется геометрической формой активной среды (см. §5.1). Поэтому в тех случаях, когда усиленная люминесценция оказывает заметное влияние на порог генерации, степень этого влияния может зависеть от толщины активного слоя.

Напомним, что в инжекционных лазерах параметр р характеризует следующие виды потерь: рассеяние и поглощение генерируемого излучения на неоднородно-стях активного слоя, дифракционные потери, поглощение света в пассивных областях, поглощение в зеркалах резонатора. Поглощение света свободными носителями в активной области входит в Kyc(v).

Обычно потери излучения в инжекционных лазерах рассчитываются в рамках электромагнитной теории плоских диэлектрических волноводов. Волноводный канал образует сам активный слой, диэлектрическая проницаемость которого е за счет более высокой концентрации свободных носителей несколько больше, чем в окружающих пассивных областях. В гомолазерах относительные изменения е невелики: Ае/е= 10-...10-. В гетеролазерах вследствие сильной дисперсии е вблизи края собственного поглощения скачок значения е на границе активной и пассивной областей на один-два порядка больше.

Важнейшей характеристикой волновода является параметр оптического ограничения Г, равный отношению потока излучения, заключенного в пределах активного слоя, ко всему потоку. Этот параметр зависит от толщины активного слоя, скачков диэлектрической проницаемости на его границах и от типа электромагнитной волны. Для симметричного волновода его можно представить как функцию безразмерной приведенной толщины слоя

(2.22)

где К - длина волны излучения в активной среде.

Из расчетов следует, что для каждого типа волн, кроме нулевого, существует критическое значение 01. Если D <Окр, то локализация волны отсутствует. С ростом D выше Окр параметр Г резко возрастает и приближается к единице при D, равной нескольким единицам.

Чем больше значение Г, тем меньше потери света в волноводе. Из (2.21) следует, что при одинаковом значении й/Х в гетеролазерах Z)* и Г будут значительно больше, чем в гомолазерах. Высокое качество волноводов в гетеролазерах связано еще и с тем, что пассивные области имеют большую ширину запрещенной зоны, чем активный слой, поэтому генерируемое излучение в пассивных областях поглощается слабо.

Из приведенных соображений вытекает, что как в гомолазерах, так и в гетеролазерах, кроме лазеров на гетероструктурах с раздельными оптическими и электронными ограничениями, имеется некоторая оптимальная толщина активного слоя йот, при которой порог генерации минимален. В лазерах с й<.йот порог повышается вследствие ухудшения волноводных свойств активного слоя. Если й> йот, то порог растет из-за уменьшения концентрации электронов и дырок в активной области. Кроме того, он может возрасти в результате повышения уровня усиленной люминесценции при больших й.

В гетеролазерах с раздельными электронным и оптическим ограничениями достигается наименьший порог генерации, поскольку толщина активного слоя может быть сделана значительно меньше йот без увеличения дифракционных потерь, которые определяются не размерами активного слоя, а толщиной волновода, образованного активным слоем с прилегающими к нему широкозонными и прозрачными для генерируемого излучения слоями (см. рис. 2.3,(3).

Рекордно малые значения порогового тока получены в лазерах на квантоворазмерных слоях как вследствие малой толщины активной области, так и благодаря высокосовершенной технологии изготовления таких слоев. В частности, порог генерации гетеролазера на основе AIGaAs с многослойной квантовой ямой и толщиной слоев 5...7 нм равен 2,4 мА при комнатной температуре и 0,88 мА при 77 К (Н. Furuyama et al., 1986). Толщина волноводного слоя в этом лазере равна 150 нм.

Зависимость порога от коэффициента потерь. Один из возможных механизмов рекомбинации в полупроводниковом лазере связан с межзонными переходами. При расчетах обычно используют модель параболических зон. Такое приближение оказывается, по-видимому, достаточно хорошим при высоких температурах и большой величине коэффициента потерь, когда роль хвостов

плотности состояний, образующихся при сильном легировании, незначительна.

В модели параболических зон с правилами отбора по волновому вектору коэффициент поглощения

/C(V) = -}-Bg(v) [/е(£.) -/e(£.)]/lV = = K(v)[/e(f.)-/e(£.)],

(2.23)

a мощность спонтанного испускания можно представить в виде

Wc„(v)=g(v)/e(f.) [l-/e(f«)]/lV, (2.24)

где А и В - коэффициенты для вероятностей спонтанных и вынужденных переходов;

giv)=4Kh(-y\hv-Egy (2.25)

- приведенная плотность состояний; тг = тетн(т-\---тл)~ - приведенная масса носителей; и т,,- эффективные массы электрона и дырки соответственно. Функция Ферми - Дирака выражается формулами (1.29). Разность \-fe{Ev) равна вероятности заполнения уровня энергии £„ дыркой; ><. = Bg (v) hv/Vg - предельное значение коэффициента поглощения.

При отсутствии тока, проходящего через диод, fe{E„)> fe{Ec). Коэффициент поглощения положителен во всем спектральном интервале и равен B{hv - Eg)/Vg. Система находится в термодинамическом равновесии

и Fe=Fh = Fo.

Если через диод пропускать ток, то в зоне проводимости увеличивается концентрация электронов, а в валентной зоне - концентрация дырок. В активном слое вблизи р - п-перехода (см. рис. 2.2) уровень Ферми Fq как бы расщепится на два квазиуровня Ферми, расстояние между которыми будет увеличиваться с ростом тока (рис. 2.7). Когда значение AF становится больше ширины запрещенной зоны, возникает усиление в интервале энергий AF - Eg. Частота v„hb = AF/h называется частотой инверсии, поскольку она служит границей перехода от усиления к поглощению: при v<v„„b /c(v)<0, а при v> Vhhb /c(v)>0. Деформация спектра поглощения по мере возбуждения показана на рис. 2.8.

Рис. 2.7. Увеличение разности между квазиуровнями Ферми с ростом тока в однородном слое

Если коэффициент потерь резонатора не зависит от частоты, то условие стационарной генерации /Cyc(v) =к„ будет выполняться в максимуме коэффициента усиления (максимуме коэффициента поглощения). Как видно из рис. 2.8, с ростом частота генерации увеличивается. Для любого заданного значения /с„, не превышающего максимально возможное значение коэффициента усиления данной системы, можно подобрать уровень возбуждения, задаваемый величинами и Ff, так, чтобы удовлетворить условию стационарной генерации.

Квазиуровни Ферми не являются независимыми величинами. Они связаны между собой уравнением электронейтральности. В собственном полупроводнике оно означает равенство чисел электронов и дырок п = р, или

gc(Ec)fe(Ec)dEc =

= \ g„(£„)[l-fe(£.)]df„.

(2.26)

где функции плотности состояний для модели параболических зон имеют вид

.(£.)=4я(-) (£,-£,о)/2.

g„(£„)=4n(-) (£„о-£.)1

(2.27)

Интегрирование проводится по всем энергиям зоны проводимости и валентной зоны.

В общем случае интегралы (2.26) не выражаются аналитическими функциями. Поэтому уравнение (2.26) решается численными методами и Fe находится как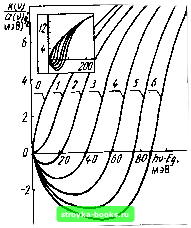

Рис. 2.8. Деформация спектра поглощения при пропускании тока через диод:

0-1 = 0, / -6 - /</2</з</4</5<

</б. На вставке показаны те же кривые для большего интервала значений

функция Fk или наоборот. Уравнение (2.26) позволяет найти значения Fe и Fh, при которых /Cyc(v)=/Cn. После этого рассчитывается порог генерации, который с учетом (2.20), (2.23) и (2.24) представляется в виде

. Aned (2m,kT\

[exp(m,x/me-Се) + 1] [ехр(т,х/тл -л)-f 1]

(2.28)

Здесь введены обозначения; Тсп = т1л/>4 - время жизни носителей, определяемое вероятностями спонтанных переходов; х= (hv - Eg) /кТ; 1= {F F со) / кТ, /,= (£„0 - - Fh) /кТ; учтено, что Ее и связаны законами сохранения энергии и импульса и однозначно определяются частотами

Ec = Eco+{){hv-Eg),

(2.29)

Минимальное значение пороговый ток имеет в идеальном резонаторе, коэффициент потерь которого «„ = 0. При меньших токах усиление отсутствует, при больших -