
 |
|
Главная Усиленная люминесценция [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [ 14 ] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] 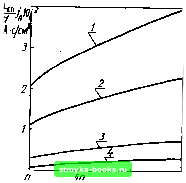 Рис. 2.9. Зависимость порога генерации от коэффициента потерь к„ в модели параболических зон с правилом отбора по волновому вектору для компенсированного GaAs при температуре 300 (/), 200 (2), 80 (5), 40 К (4) коэффициент поглощения становится отрицательным. Плотность этого тока будем называть плотностью тока инверсии и обозначать /ннв- Результаты численного расчета зависимости порогового тока от коэффициента потерь для компенсированного полупроводника с параметрами GaAs приведены на рис. 2.9. Видно, что при увеличении коэффициента потерь от нуля до 150 см~ порог превышает \,kb не более чем в два раза. Ток инверсии при высоких температурах достигает больших значений. Для d = 2 мкм, Тсп=10" с из графиков находим /«нв (7 = 80 К) =600 А/см, (7- = 300 К) =2100 А/см1 Начальные участки кривых /, 2 на рис 2.9 можно аппроксимировать формулой (2.30) где р~ -коэффициент пропорциональности; <1. В дальнейшем зависимость /п от Кп становится линейной и удовлетворяет формуле (2.31) /n = io-fP Кп. Параметр jo равен отрезку, который отсекает прямая (2.31) на оси /„. Формула (2.31) дает правильное значение порога только на линейном участке кривой /п(к:п), поскольку при Кп-*-0 /п стремится к /„„в, а не /о. Из расчетов следует, что для модели параболических зон как с правилом отбора по волновому вектору, так и без правила отбора при больших зависимость /ц от /Сп вновь может стать нелинейной и аппроксимиро-
Рис. 2.10. Зависимость параметра /о от выбора участков кривой /„(/с„), которые аппроксимируются прямыми линиями (2.31) ваться соотношением /„ = /о + р-<, (2.32) причем ц> \. Ток инверсии и параметр /о. Формула (2.32) отличается от (2.30) не только значением показателя степени q. Главное отличие заключается в том, что параметр /о по физическому смыслу и величине, как правило, не совпадает с /„«в. Инверсный ток - это порог генерации в резонаторе с Кп = 0. Величина /о появляется в теории как параметр аппроксимации. В зависимости от участка кривой /„(/Сп), который аппроксимируется функциями (2.31) или (2.32), значение \о может быть больше, равно или меньше /„„в. При всегда положительном /„„в возможно отрицательное значение /о. Это проиллюстрировано на рис. 2.10, где показаны различные варианты аппроксимации некоторой условной кривой /п(/Сп) прямыми линиями (2.31). В двух случаях параметр /о совпадает с /инв- Во-первых, если аппроксимируется начальный участок кривой /п(/Сп), как показано на рис. 2.10. Во-вторых, если во всем исследуемом интервале значений /Сп, начиная с /Сп = 0, пороговый ток линейно зависит от Кп. Строго говоря, ни один из этих случаев не реализуется на опыте. Поэтому при интерпретации экспериментальных данных необходимо учитывать отличие параметра /о от /„нв. Параметр /о относится к числу самых важных характеристик лазерного диода. Он входит в выражения для коэффициента усиления, порога, мощности и КПД генерации, в формулы, описывающие усиленную люминес- ценцию, нестационарный режим генерации и т. д. Инженерный расчет полупроводниковых лазеров как инжекционных, так и с оптической и электронной накачкой невозможен без учета /о. Опыты показывают, что во многих случаях величина /о сравнима с порогом генерации. Максимальный коэффициент усиления. Формулы (2.30) -(2.32) справедливы при условии, что коэффициент потерь резонатора равен максимальному по спектру значению коэффициента усиления к". Следовательно, до порога генерации зависимость к" от плотности тока можно представить в виде * -•ус = Р(/-/о), (2.33) (2.34) где n=l/q может быть больше и меньше единицы. Поскольку параметр 3 определяет увеличение коэффициента усиления с ростом плотности тока на единицу, его называют удельным коэффициентом усиления. При достижении порога генерации максимальный коэффициент усиления становится равным коэффициенту потерь и не зависит больше от тока, если только /Сп = const. В резонаторе с селективными потерями, где Kn(v) сильно зависит от длины волны излучения, частота генерации определяется точкой касания кривых (c„(v) и «;yc(v) (рис. 2.11), а приведенные выше формулы неприменимы. * в литературе иногда применяются эмпирические формулы для порога и коэффициента усиления в активной области /„=P"/C„ = p-(/C,-f (X), «:ус = Р/, (2.35) (2.36) где а отождествляется с коэффициентом оптических потерь. Формула (2.35) служит непосредственным обобщением экспериментальных данных о линейной зависимости порога от коэффициента потерь. Выражение (2.36) следует из (2.35) и энергетического условия генерации. Из сравнения (2.31) и (2.35) находим a = P;o-fp. (2.37) Следовательно, параметр а в (2.35) состоит из комбинации трех физически разных параметров. Только если /0 = 0, он определяет внутренние оптические потери, т. е. совпадает с р. 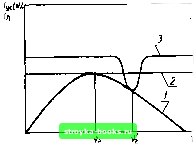 Рис. 2.11. Графики коэффициента усиления /Cyc(v) (/) и коэффициента потерь к„ в неселективном (2) и селективном (3) резонаторах Вопрос об экспериментальном определении параметра /о и его численном значении будет рассмотрен в §2.4. Поглощение излучения свободными носителями в активном слое. Подобно тому, как при вычислении коэффициента поглощения гармонического осциллятора учитываются оптические переходы между всей совокупностью бесконечного числа энергетических уровней (см. §1.2), так и для нахождения коэффициента усиления активной среды необходимо принимать во внимание все переходы, которые индуцирует генерируемое излучение. В рубине, например, возбужденные частицы, находящиеся на метастабильном уровне, совершают вынужденные переходы не только вниз, в основное состояние, но и вверх, на более высокий метастабильный уровень (триплет-триплетные переходы). Аналогичные переходы между возбужденными уровнями происходят в хелатных соединениях редкоземельных элементов и других веществах. Поглощение света свободными носителями в полупроводниках играет в процессе генерации такую же роль, как и триплет-триплетные переходы в твердотельных лазерах. Под действием внешнего излучения электроны и дырки могут либо рекомбинировать с испусканием кванта света, либо поглотить квант света и перейти на более высокие энергетические уровни в пределах зоны. Если Kc.h(v) - коэффициент поглощения свободными носителями, а (CyJ(v) - коэффициент усиления, возникающий в результате инверсной населенности в активном слое, то энергетическое условие генерации можно представить в виде Kyc(v) =(C/c(v) -Cc.h(v) =Kr + p. (2.38) 101 Величину /Cc.h(v) можно было бы перенести в правую часть равенства (2.38) и объединить с параметром р. Тогда новый коэффициент внутренних оптических потерь p = P + /Cc.h(v) характеризовал бы кроме других видов потерь и поглощение свободными носителями в активном слое. При вычислении порогового тока не имеет значения, куда включается величина /Cc.h(v): в коэффициент усиления как слагаемое с отрицательным знаком или как добавка к параметру р. В обоих случаях численные значения тока будут совпадать. Однако объединение р и /Cc.h(v) представляется нецелесообразным, поскольку в формулу для мощности генерации (2.10) входит параметр р, не включающий в себя коэффициент Kc.h(v). Кроме того, нецелесообразно присоединять к параметру величину, явно зависящую от тока. Поглощение света свободными носителями уменьшает коэффициент усиления в активной среде и обрезает длинноволновой край спектра усиления. Поэтому разность квазиуровней Ферми для электронов и дырок AF, необходимая для получения положительного коэффициента усиления, не может быть меньше некоторого минимального значения min> о, зависящего от выбранной модели вещества и температуры. Отсюда следует, что ток инверсии никогда не равен нулю, так же как не равно нулю поглощение свободными носителями в легированном полупроводнике. В собственном полупроводнике /Cc.h(v) может быть пренебрежимо малым. Но в этом случае отсутствуют хвосты зон и, как показано выше, /„„в о даже при отсутствии поглощения излучения свободными носителями. Поскольку /Cc.h(v) зависит от уровня накачки, то учет этой величины в (2.38) не только приводит к большим значениям тока инверсии, но и изменяет форму кривой /п(/Сп). В формулах аппроксимации изменяются параметры /о, Р, q, хотя сами формулы можно использовать при интерпретации результатов эксперимента. Температурная зависимость порога. Модель параболических зон позволяет описать ряд закономерностей, наблюдаемых в инжекционных лазерах. Вместе с тем она обладает некоторыми недостатками. На опыте пороговый ток гомолазеров при низких температурах практически не зависит от температуры. Расчет же в рамках этой модели не дает четко выраженного участка на кривой /п(Г) с практически постоянным значением порога. 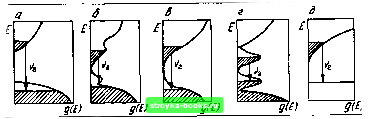 Рис. 2.12. Основные спектроскопические модели активной среды инжекционных лазеров: а - параболические зоны, б - параболические зоны сливаются с примесными зонами; в - параболические зоны с экспоненциальными хвостами Зои; г - примесные гауссовы зоны; д - дискретный уровень и экспоненциальный хвост Очевидно, при низких температурах (а при малых значениях Кп и при более высоких температурах) стимулированное испускание происходит с участием хвостов зон и примесных зон. В-теории рассчитывался порог генерации также для модели параболических зон, слившихся с примесными зонами; с учетом экспоненциальных хвостов зон; для примесных гауссовых зон; для зоны проводимости и дискретного уровня вместо валентной зоны (рис. 2.12). Во всех случаях задача решается, как для модели параболических зон: для заданного значения /Сп из уравнения электронейтральности находится связь между квазиуровнями Ферми для электронов и дырок, а затем вычисляется мощность люминесценции. В частности, для модели двух гауссовых примесных зон при низких температурах порог практически постоянен, причем с возрастанием Кп интервал температур, для которых /„(Г) неизменно, расширяется. В этом случае ширина полосы спонтанного испускания определяется распределением состояний в хвостах примесных зон. В области высоких температур /п(7) ~ Т"", где /и> 2 для малых потерь и уменьшается с их ростом. В интервале 7 = 60...240 К зависимость ]п{Т) носит экспоненциальный характер. Подобные зависимости наблюдались на опыте. Вывод о том, что участок постоянного тока при низких температурах обусловлен хвостом плотности состояний, подтверждается также результатами рассмотрения переходов между хвостами основных зон, спадающими по закону, отличному от гауссова. Влияние легирования на величину порогового тока рассматривалось для Т = 80 К. Характер зависимости [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [ 14 ] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] 0.0006 |