
 |
|
Главная Усиленная люминесценция [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [ 16 ] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] бесконечно тонкий слой dx. Мощность люминесценции слоя dx в расчете на единичный интервал частот равна Wx{v)sdx, откуда некоторая часть lW{v)sdx распространяется перпендикулярно к зеркалу 2, а вторая такая же часть - перпендикулярно к зеркалу /. Эти два потока будут многократно проходить через стержень, усиливаясь или ослабляясь в зависимости от знака разности (Кус -р) и теряя энергию при каждом отражении на полупрозрачных зеркалах. Поток люминесценции, возникший в слое dx и выходящий через вторую грань, выражается двумя геометрическими прогрессиями S2{v,x)dx = S2:{vx)dxS2{vx)dx = = g Г. (V) Sx(1 - лг)е*--[е-(1 + 9 + .• •) + = lW,{v)sdx{\-r2) (2.41) где 9 = г,Г2ехр2(Кус -p)/< 1. Интегрируя (2.41) по x от нуля до /, получаем S2л(v)=S24v)X [1-МГ2) [е""-р"-1] [г,е<--р"+11 /(1+п)(Кус-р)(1-пл2е2<"-") • -" Здесь \-ГхГ2 (2.43) - поток люминесценции, выходящий через зеркало 2 стержня (см. рис. 2.13) при условии, что Куе -р = 0. Контур SL(v) совпадает со спектром люминесценции, не искаженным поглощением и усилением люминесценции в активной среде. В диодах с малой шириной активной области S2л(v) соответствует спектру люминесценции, выходящей из боковых граней резонатора. Если измерить на опыте S2л(v) и SL(v), то с помощью формулы (2.42) можно рассчитать значение Кус -р для всех значений V в пределах полосы усиления. Коэффициент потерь люминесценции. Плотность энергии люминесценции в активной среде определяется скоростью рекомбинации в каждой точке активной среды, усилением и потерями излучения. Степень усиления зависит от размеров активной среды и коэффициентов отражения на ее границах. Потери люминесценции связаны либо с выходом за пределы резонатора, либо с поглощением в резонаторе. В теории твердотельных лазеров показана возможность расчета плотности радиации на основании уравнений переноса. Даже в линейном приближении задача оказывается весьма сложной и до сих пор решена только для простейших частных случаев. Поэтому перспективными и целесообразными представляются полуэмпирические методы исследования. В теории сравнительно легко получить общие формулы для плотности радиации. Входящие в эти формулы параметры необходимо определить на опыте. Одним из таких параметров является коэффициент потерь люминесценции Кд, аналогичный коэффициенту потерь Кп для генерирующих мод. Однако в отличие от к„ величина Кл имеет смысл среднего значения некоторой функции, зависящей от координат вещества и направления распространения излучения. Для усиленной люминесценции, распространяющейся перпендикулярно к зеркалам плоского резонатора, к„ выражается формулой (1.57), и при v = Vr имеем Кл = Кп. В стационарном режиме поступление люминесценции компенсируется ее потерями. С помощью параметра Кл уравнение баланса для люминесценции можно представить в виде rл(v)+ \ УgKyc(v)aл(v)dV = = Кл \ VgUjt{v)dV. (2.44) Вынося за знак 1Йтеграла в (2.44) среднее по объему значение Kyc(v), получаем среднюю плотность люминесценции Uл(v) = rл(v) (2.45) с помощью (2.45) по известным из опыта значениям Wл(v) и Kyc(v) можно рассчитать плотность люминесценции Uj,{v). Так как Wл(v) =hv \ rjt{v)dV, где Лл(v) - скорость спонтанной рекомбинации в расчете на единичный спектральный интервал, то с помощью (2.45) находим скорость рекомбинации, стимулированной люминесценцией: J hv Г /Сус(у)Гл(у) 3 /Сл -/Сус(у) (2.46) Исследование коэффициента потерь позволяет связать лазерные характеристики диода с его геометрией, состоянием боковых поверхностей, оптическими и волно-водными свойствами активной области. Рассчитано значение /Сл для диода с идеально матированными торцевыми и боковыми гранями и полностью поглощающими пассивными областями. Из расчетов следует, что /Сл уменьшается с ростом площади р - п-перехода примерно как /Сл~1/У5, где s - lw. Поскольку коэффициент потерь /Сп тоже уменьшается как 1 , то неравенство Кл > Кп выполняется только в некотором интервале длин. Диод может генерировать, если его длина заключена в пределах /min <1 / <С /max, для которых Кл> /Сп. Границы изменения / раздвигаются, если ширина диода уменьшается. С ростом р значения /„ах и /глш сближаются и для некоторого предельного значения рпр генерация аксиальных мод вообще невозможна. Влияние усиленной люминесценции на порог генерации. Формула (2.15) в общем виде дает зависимость порога генерации от скорости рекомбинации, индуцированной усиленной люминесценцией. Однако при расчете порогового тока для различных механизмов оптических переходов в полупроводниках до сих пор скорость усиленной люминесценции Рул не учитывалась. Возвращаясь к формуле (2.15) и учитывая (2.46), для плотности поро- гового тока будем иметь /п = /пО \[/Сус(у) rл{v)/(/Сл - /Сус(у))] dv \ rл(v)dv , (2.47) где /по - плотность порогового тока при Яул = 0, подробно исследованная в § 2.3. Второе слагаемое в (2.47) в зависимости от знака коэффициента усиления распадается на две части: положительную и отрицательную. Первая часть дает увеличение порога генерации из-за роста скорости рекомбинации, вызванной усиленной люминесценцией. Отрицательный член характеризует роль той части люминесценции, которая поглощается в активной области и увеличивает инверсную населенность. Эта часть люминесценции служит дополнительной оптической накачкой кристалла. С увеличением квантового выхода люминесценции ее роль возрастает. Если в пределах спектра люминесценции коэффициент потерь /СлЗ>/Сус(у) и слабо зайисит от у, то выражение (2.47) упрощается: /п = /по(1+Т1л-) , (2.48) где /Сус - эффективный коэффициент усиления, полученный путем усреднения /Сус(у) по спектру люминесценции. Формула (2.48) позволяет оценить относительный вклад усиления и поглощения люминесценции в пороговый ток. При /Сус> О преобладает усиленная люминесценция. Если /Сус<0, то более существенна оптическая накачка люминесценцией. Как видно из (2.48), если /Сл-/Сус(у), то порог генерации стремится к бесконечности. Схематически зависимость /п от /Сл -/Сп представлена на рис. 2.14. Кривая / соответствует малым положительным значениям /Сус, когда для больших /Сл оптическая накачка преобладает над дополнительной рекомбинацией, вызванной усиленной люминесценцией. Если значение /Сус(у) велико и решающую роль играет усиленная люминесценция, то значение /п всегда больше /по и монотонно растет с уменьшением Кл (кривая 2). 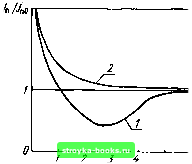 Рис. 2.14. Зависимость плотности порогового тока /„ от коэффициента потерь усиленной люминесценции к„: 1 - оптическая накачка люминесценцией преобладает над усилением люминесценции; 2 - усиление люминесценции играет решающую роль K,fHn,omH.ed В случае, когда максимальный коэффициент усиления линейно связан с током, плотность порогового тока можно представить в виде суммы /по и некоторой добавки, зависящей от усиленной люминесценции. Обозначая максимальное значение коэффициента усиления при /?у.л = 0 как /Сус, получаем Р(/-/о) Здесь F(i,Uji) - функция плотности тока и Ил, которую во многих случаях можно аппроксимировать произведением параметра нелинейности а на u. F Ц, и) = аи. При пороговом токе /Сус = /Сп, поэтому из (2.49) следует /п=/0+Г [!+/(/, «л)]/Сп = = /no + p~f (/п, ил)/Сп. (2.50) Варьируя плотность люминесценции в диоде, например путем изменения его длины и ширины, можно легко экспериментально исследовать и оценить нелинейные свойства системы. Лазер с непланарным р-п-переходом. Из всех видов лазеров инжекционные полупроводниковые квантовые генераторы стоят на последнем месте по мощности генерации как в импульсном, так и в непрерывном режиме. Этот недостаток сужает область их практического применения. Поэтому продолжаются поиски путей повышения мощности излучения полупроводниковых лазеров. Для получения мощного лазерного луча предложено несколько способов суммирования излучения большого числа маломощных лазеров. Однако лазерные системы в виде стопы р - л-переходов или матриц, состоящей In, кА/ш 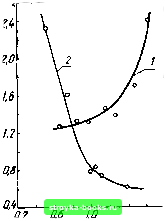 Рис. 2.15. Зависимость порога генерации аксиальных (/) и неаксиальных (2) мод инжекционного лазера на основе GaAs от ширины диода w при Г = 80 К (Г. И. Рябцев, В. П. Грибковский, В. А. Самойлюкович, 1974 г.) fA w, мм ИЗ отдельных излучателей, дают в целом некогерентное излучение и могут применяться в тех елучаях, когда решающее значение имеет только направленность и монохроматичность света, а не его когерентные свойства. Некоторые новые возможности для повышения мощности когерентного луча открывают многолучевые лазеры, состоящие по существу из большого числа диодов, объединенных одной подложкой и связанных генерируемым излучением, которое частично, проходит через все диоды. В принципе работу по увеличению мощности когерентного луча можно вести в двух направлениях. Во-первых, путем улучшения качества лазера увеличивать съем энергии излучения с единицы объема активной среды и, во-вторых, увеличивать сам генерирующий объем. В полупроводниковых лазерах возможности значительного увеличения удельной мощности генерации Wv (Вт/см) практически исчерпаны. Например, в инжекцион-ном лазере с типичной площадью р - /г-перехода порядка s=10~ см и толщиной активной области d= \ мкм уже при мощности генерируемого луча Sr= Ю Вт имеем Wt = = Sr/sd7si\0 Вт/см. Плотность выходящего потока излучения столь высока, что на зеркалах резонатора образуются выколки и наступает деградация всего объема активной области. По этой причине представляется нецелесообразным значительное увеличение длины диода или разработка любых других конструкций, в которых будет достигаться более высокая плотность потока излу- [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [ 16 ] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] 0.0009 |