
 |
|
Главная Усиленная люминесценция [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [ 19 ] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] что через активную область будет проходить ток некоторой заданной плотности /. Имеется возможность варьировать длину активной области и тем самым изменять коэффициент потерь резонатора. В некоторых случаях Кп изменяют путем нанесения диэлектрических покрытий или погружением диода в иммерсионную жидкость, что приводит к изменению коэффициента отражения зеркал. Например, при нормальном падении излучения и отсутствии поглощения на границе раздела двух сред с показателями преломления п и П2 коэффициент отражения \ П1 + П2 / Если диод находится на воздухе, то П2= 1 и для п = 3,6 имеем гж0,32. Для диода в укропном масле с П2=1,54 находим г ж 0,16. При этом коэффициент потерь Кг согласно (1.58) увеличивается в 1,6 раза. Найдем значение коэффициента потерь, при котором объем энергии с единицы длины диода будет максимальным. Рассмотрим выражение для мощности генерации в линейном приближении, когда выполняется соотношение (3.2), а зависимость порогового тока от коэффициента потерь задается формулой (2.31). Такое приближение имеет широкие границы применимости и справедливо в больших интервалах изменений тока и коэффициента потерь. Подставляя (2.31) в (3.2), приходим к развернутой формуле для мощности генерации: 5r = sri.[/-/o-r(c. + p)] (3.5) При неизменных других параметрах и / = const мощность генерации с увеличением длины диода / вначале возрастает, а затем стремится к своему предельному значению. Насыщение достигается, когда Кг становится меньше р. Обозначая ширину диода w = s/l, из (3.5) получаем lim Sr = w--Пг(/ -/о-Р~р) In (1/ПГ2) 2р (3.6) В условиях насыщения рост мощности генерации в активном слое вследствие увеличения длины диода полностью компенсируется увеличением внутренних потерь. В то же время мощность генерации в расчете на единицу длины Sr как функция Кг при / = const имеет максимум. Его положение легко найти, если производную от Sr по Кг приравнять к нулю. Это приводит к условию кГ= л/Р(/-/о)р-Р= л/-р, (3.7) где к° равно тому максимальному коэффициенту усиления в активной области, который был бы при заданном токе и отсутствии генерации. Условие (3.7) справедливо и для твердотельных лазеров. Максимальный КПД при j=const. Обозначим U напряжение, приложенное к р - п-переходу, а Ro - последовательное сопротивление диода в расчете на 1 cм, с помощью (3.5) получим выражение для КПД инжекционного лазера: 11г = = Tlr s{jU + Roj) hvr /-/о-P~(« + p) e jU + Roj Kr + p (3.8) Условие работы лазерного диода с максимальным КПД при заданной плотности тока и слабой зависимости т]г от Кг имеет вид (3.7). При этом максимальный КПД Jl (V"/-Vp7p7) i+Roi/v Tlmax -Tlr -JJ- (3.9) Кривые, рассчитанные по формуле (3.9), приведены на рис. 3.5. Максимальный КПД при заданном / существенно зависит как от последовательного сопротивления диода Ro, так и от коэффициента внутренних оптических потерь р. Для малых значений Ro и р достигается высокий КПД при сравнительно небольших токах. Когда р~1 см~, i?o~10~ Oм•cм и т]г=1, можно ожидать КПД около 80%. Однако реальные значения ц ограничиваются величиной т]г, которая обычно меньше единицы. Плотность тока при максимальном КПД диода и Кп = const. Если предположить, что с ростом тока накачки коэффициент потерь резонатора и внутренний квантовый выход генерации остаются неизменными, то КПД лазера будет однозначной функцией / и достигает своего максимального значения т]тах при некотором /max. 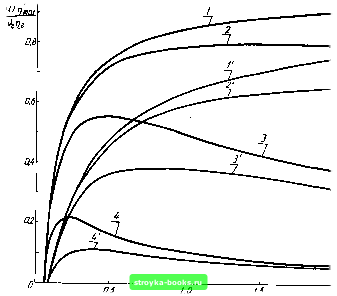 Рис. 3.5. Зависимость максимального КПД ri,, от плотности тока / ,„ = 600 A/c, p = 3.:l. Ю- е«/А; ,,= 1 см- <,-4), р= ,0 см- ,С. ,Г, 4): К„ = 0 Ov,..„» (1, I), R„=\0 Ом.см (2, 2). йо=10-< Ом-см (3. З), Я«=\0- Ом-см (4, 4) Приравнивая производную dr\(j)/dj к нулю, где ti(/) задается формулой (3.8), находим bax=/n(l+VT+t/0/n), (3.10) <ах = Т1г (Vr+/?0/n/[/-V0/n/[/)2. (3.11) Согласно (3.10) с ростом порога значение /max увеличивается, а отношение /тах п понижается, т. е. максимальный КПД достигается при меньшем числе порогов. Кривые, рассчитанные по формуле (3.11), показаны на рис. 3.6. При некотором оптимальном коэффициенте полезных потерь к"" получается наибольший КПД для лазерного диода с заданными параметрами. Иногда при оценках наибольших значений мощности генерации и КПД в функции выхода (3.4) вместо параметра р используется величина а, которая берется из экспериментальных данных по зависимости /„ от Кг. Подобные оценки справедливы только в том случае, 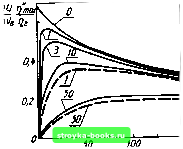 Рис. 3.6. Зависимость riax от коэффициента потерь к,: ,0 = 500 А/см. р = 3.3.0- см/А, Ка/и = 7-\0- см/А; цифры около кривых - значения р, см : штриховые линии построены по формуле (3.4) при замене р в функции выхода (3.4) величиной a = p-f (i/o когда параметр /о = 0 (см. §2.3). Очевидно, пренебрежение параметром /о может привести в некоторых случаях к существенной ошибке в определении оптимального значения к"" и в оценке предельных значений мощности генерации и КПД. Это особенно заметно для малых р (см. рис. 3.6). Предельный КПД генерации. Совокупность значений КПД как функция коэффициента потерь Кг и плотности тока образует поверхность в пространстве т], Кг, /. Наивысшая точка этой поверхности определяет предельный КПД генерации r\. Условие предельного КПД определяется при постоянстве остальных параметров равенством нулю частных производных от т] по / и Кл и сводится к системе двух уравнений (3.7) и (3.10). Подставляя (3.10) в (3.7) и обозначая л;=к°" + р, приходим к уравнению четвертой степени .-2р.з р2р„(2+).- (3.12) Решение этого уравнения, полученное методом понижения степени, имеет вид x=-e-{l+vг+"y[(l+VГ+y)+ + 2 m2 + U/Roh)/9-y 2yf П (3.13) 1/3 . 1 / pt/ V (3.14) +0+)0+)]- Зная внутренние параметры лазерного диода и подставляя их значения в (3.13) и (3.14), можно определить величину к°"\ а по (3.7) или (3.10) - плотность оптимального тока, при которых инжекционный лазер будет работать с предельным КПД. Введя обозначение ф = = (io + x)Ro/V, формулу для предельного КПД представим в виде Формулы (3.13) и (3.15) упрощаются, если выполняется условие p<P/o/Vl + t7Wo- В этом случае х = = AJpio-U/Rojo, а (p = Rojo/U. Тогда Выражение (3.16) позволяет оценить верхний предел для КПД лазерного диода при заданных параметрах. Уменьшение последовательного сопротивления Rq особенно важно для полупроводников с малой шириной запрещенной зоны и при высоких температурах, когда значение /о быстро растет. Уменьшение любого из параметров Ro, р, j„ и приводит к увеличению предельного КПД. Величина к™" убывает с уменьшением р, р, jo и увеличением Ro. При малом р значение т]пр практически не зависит от /о. Для больших р зависимость rjnp от /о становится сильнее, а от р - слабее. Анализ формулы (3.15) показывает, что высокий предельный КПД достигается при больших Кг и, следовательно, для диодов малой длины. Это значит, что такие диоды будут давать небольшие мощности генерации. Для получения значительных мощностей необходимо, как следует из (3.5), увеличивать размеры диода. С увеличением длины, однако, поток генерируемого излучения 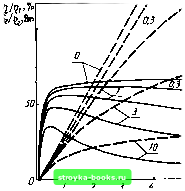 Рис. 3.7. Зависимости КПД Г) (сплошные линии) и мощности генерации (штриховые линии) от длины диода /: ;г„=10- Ом-см У=1,5В; ш = = 0 05 см; п =г2 = 0,32; Avr= 1.5 эВ; / = 5000 А/см io = 500 А/см"; (i=3-l0" см/А; цифры около кривых - значения р, см" приближается к некоторому предельному значению, определяемому формулой (3.6). Существенное влияние на величину предельной мощности при заданных j и w оказывает коэффициент внутренних потерь р. Например, при • = 5000A/cм, /о = 500 A/cм, p = 3•10- см/А, Г = Г2 = 0,32, /ivr=l,5 эВ, ау = 0,05 см и Т1г = 1 для р = = 10 см" находим предельное значение мощности генерации Sr = 36 Вт. Для р = 1 см это значение Sr = 382 Вт. Но получить мощности, близкие к предельным, в случае малых р можно только для длинных диодов, изготовление которых связано с большими технологическими трудностями. Имеется также ограничение длины диода снизу. Она должна превышать минимальное значение /min, определяемое выражением n,in=ln-i-/[P(i-/o)-pl. (3.17) Предельный КПД получается при сравнительно малой мощности генерации. Для р<1 с увеличением длины от предельного значения до 5 мм КПД уменьшается незначительно (рис. 3.7), в то время как мощность генерации возрастает почти на 90 Вт. Для больших р с увеличением / КПД уменьшается существенно, а 5г возрастает на меньшую величину. Таким образом, для малых р путем увеличения длины можно получить достаточно большую выходную мощность, а КПД при этом будет мало отличаться от предельного значения. При оценке использовались наиболее типичные параметры GaAs. [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [ 19 ] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] 0.0009 |