или просто пропусканием, называется отношение потока излучения, пропущенного данным телом, к потоку излучения, упавшего на него. Очевидно, в анализе работы лазеров с оптической накачкой поток возбужденного излучения, пропущенный активной средой, необходимо рассматривать как потери энергии, снижающие КПД генерации.

Если коэффициент поглощения не зависит от накачки и к=const, то для пропускания т плоскопараллельной пластины толщиной d при помощи расчетов с учетом многократных отражений от передней грани (харакгери-зуются коэффициентом отражения ri) и задней грани (характеризуются коэффициентом отражения Г2) получаем (см. рис. 1.7, а)

r = S,/So= (l-O (1-2) exp (-.0)

1 - Г1Г2ехр ( -2/cod)

Для типичных значений Г[ = Г2 = 0,37 и й! = 0,04 см, подставляя в (5.13) /со=10, 10, 10 см~, находим соответственно т=0,28; 0,007; 1,7-10-".

В лазерах с оптической накачкой плотность потоков возбужденного излучения достигает больших значений, а коэффициент поглощения в общем случае нельзя считать постоянным. Возможно как просветление, так и затемнение активной среды на частоте возбуждения. Связь между So и Sj становится более сложной и выражается громоздкими формулами, которые получаются из решения уравнения Бугера (см. формулу (1.2)):

K(S)S

= -d.

(5.14)

Для K{S), задаваемого формулами (1.42), (1.48), (5.12) и некоторыми другими, выражение (5.14) сводится к табличным интегралам и легко рассчитывается.

Простая и практически важная формула получается для двухфотонного возбуждения полупроводника в области прозрачности, когда K(S) =2S + p, где р характеризует небольшие по величине оптические потери и не зависит от плотности возбуждения. В этом случае из (5.14) имеем

ехр i-pd)

S11 = So

1+ [1-ехр (-pd)]p2So/p

(5.15)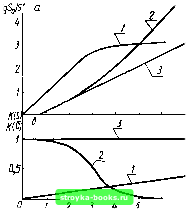

Рис. 5.3. Зависимости плотности потока 5, пропущенного образцом (а), и коэффициента поглощения K(S) (б) от So:

l-K(S)=pS. 2-K(S)=Ko(l-b

+ aS}-; Л-K = const; S.10" = -I/Pd (/1; S.10 = l/a (2»

6 IgSolS

Формула (5.15) характеризует пропускание слоя без учета отражения на его поверхностях. На опыте это можно реализовать, если нанести на поверхности пластины селективные просветляющие покрытия так, чтобы на частоте возбуждения ri и лг были равны нулю. На частоте генерации обычно titO и ггтО. Слагаемое 32S может относиться как к двухфотонному поглощению, так и к поглощению свободных носителей, поскольку концентрация свободных носителей, а следовательно и Кен, часто прямо пропорциональны плотности возбуждающего света.

Если 32 = 0, из (5.15) следует обычный интегральный закон Бугера (см. формулу (1.1)). Если, наоборот, р = 0, то

= 1+MSo • -

Согласно (5.15) с увеличением So от О до оо значение Sd растет вначале линейно с So, а затем наступает насыщение. График Sd как функции So выходит на горизонтальный участок (рис. 5.3). Следовательно, практически прозрачные первоначально пластинки с двухфотонны.м поглощением могут быть использованы как ограничители света. При любом значении плотности внешнего потока они пропускают не более

Jim Sd = p [exp(pd) - 1]

(5.16)

Если pfl(<l, то

lim Srf=l/M-

Пластины со значением р> 10 см" в качестве ограничителя света не подходят, так как зависимость 5а{5<,) выходит на насыщение для значений Sd, превышающих порог разрушения поверхности образца.

Для сравнения на рис. 5.3 приведены графики зависимости Sd(5o), относящиеся к материалам, у которых К{5) выражается формулой (1.42) и /С(5) =-. oust.

Поскольку коэффициент поглощения вещества можно представить как сумму постоянной, убывающей и возрастающей частей, то приведенные на рис. 5.3 три частных случая позволяют качественно анализировать наблюдаемые на опыте более сложные зависимости Sd от So.

§ 5.2. ЭНЕРГЕТИЧЕСКИЕ ХАРАКТЕРИСТИКИ МЕЖЗОННОЙ И ПРИМЕСНОЙ ГЕНЕРАЦИИ

Порог генерации с учетом насыщения поглощения.

Рассмотрим вариант накачки, когда возбуждающее и генерируемое излучения распространяются во взаимно перпендикулярных направлениях (см. рис. 5.1, а). В этом случае можно ограничиться первоначально рассмотрением генерации в тонком слое, в пределах которого накачка постоянна. В пластинчатых лазерах толщиной 1...2 мкм такой слой будет охватывать весь генерирующий объем.

В стационарном режиме генерации справедливы уравнения

/?в = /?г + /?л + /?б. Кус (Vr) = Кп,

(5.17)

где /?в, Rr, Ra, Re - по-прежнему скорости возбуждения, генерации, люминесценции и безызлучательной рекомбинации соответственно.

При накачке достаточно узкой спектральной линией скорость возбуждения связана простым соотношением с коэффициентом поглощения k(vi,S) на частоте возбуждения vi и плотностью возбуждающего излучения

\jK{v,S)S{v)dv=jK(vuS)S

Минимальное значение S = S„, при котором удовлетворяется условие Kyc(vr)=Kn и Rr = 0, будет порогом.

Результаты расчетов зависимости коэффициента усиления от уровня возбуждения, проведенные для инжекционных лазеров, можно использовать и в теории для лазеров с оптической накачкой. Из сравнения (2.14) с (5.17) следует, что эти уравнения без учета усиленной люминесценции и г]=\ переходят друг в друга, если произвести замену

Rsj/ed.

Следовательно, при межзонной и примесной рекомбинации, когда справедливо выражение (2.33), в отсутствие резонатора для максимального по частоте коэффициента поглощения будем иметь

Kyc(v)=p,(/?b-/?b).

(5.18)

Здесь параметры р, и RI соответствуют аналогичным параметрам (см. § 2.3) для инжекционных лазеров

pi-edp, Rl~jo/ed.

Пусть под действием возбуждающего излучения коэффициент поглощения на частоте vi уменьшается по произвольному закону

k(v,)=k"(v,) [l+f(v,,S)]-.

Тогда на основании (5.17) и (5.18) находим выражения для пороговой скорости п и пороговой плотности возбуждающего потока S„:

(5.19) Кп, (5.20)

/?n = /?b + Pl кп,

l+f(VbSn) l+f(v,,S») P.K°(V,)

где So связано с rI уравнением So = /?Bftvi/K(vi, So).

Согласно (5.20) если в инжекционных лазерах пороговая скорость накачки линейно растет с коэффициентом потерь, то при оптической накачке /?в также будет линейной функцией Кп, а пороговая плотность потока связана с Кп более сложным соотношением. Линейная зависимость будет только при отсутствии насыщения поглоще-

Рис. 5.4. Зависимость пороговой плотности возбуждающего потока 5„ от коэффициента потерь к„ для So = = 3 кВт/см, /iv,/PiK(v) = = 0,2 кВт/см при значениях параметра нелинейности а = 0 (/); 0,01 (2); 0,05 (3); 0,1 cmVkBt (4)

5п. Вт/см

80 60 40 20

ния, когда f(viS)=0. В этом случае

Для инжекционных гомолазеров на основе GaAs при 77 К типичны следующие значения параметров: /о = = 500А/см2, р = 3-10-2 см/А, d = b-\Q-* см, что соответствует величинам /?в = 6,25-10" см-з-с-, Pi = = 2,4-10 см-с. При оптическом возбуждении (/ivb = = 1,5 эВ = 2,4-10- Дж, /c°(vb)=200 см-) из (5 21) находим So = 3 кВт/см Sn=(3 + 0,2/c„ см) кВт/см2, где /Сп выражено в обратных сантиметрах.

Чтобы учесть влияние насыщения на порог генерации, необходимо задать в явном виде зависимость к{\,5). Для простейшего случая (1.42), когда f(vb, S°) =aS", из (5.20), вводя обозначение So = /iv„/?b c° (vb), находим S = o + WPi«°(vb) " l-a[5o + /iVB/c„/p,/c°(vB)] •

Как видно из последней формулы, при малых а по-прежнему должна наблюдаться линейная зависимость порога от коэффициента потерь. С увеличением отрицательного члена в знаменателе (5.22) отклонение от линейной зависимости резко возрастает (рис. 5.4). В пластинах, где не выполняется неравенство

а< [So + /iVB/Cn/Pi/c° (vb)],

генерация невозможна при любом уровне возбуждения.

Мощность и кпд генерации. В тех случаях, когда в инжекционных лазерах мощность генерации линейно

зависит от плотности тока, при оптической накачке сумму скоростей люминесценции и безызлучательной рекомбинации можно представить в виде

/?л + /?б = /?п + 7(/?в-/?п),

(5.23)

где у - безразмерный параметр (см. §3.1).

Подставляя (5.23) в (5.27), учитывая (1.42), (2.9), (2.10), равенство Sb = /?b/ivb c(Vb, S) и вводя обозначения = /iVb/Pi/Co(Vb), 6=Vrr/C(vb)u!/c7VB(/Cr + p), нзходим

полный поток генерируемого излучения

S, = wld{\\-a(So + Ik,) ] Sb- (So + 1к„)\, (5.24)

где по-прежнему w м I - ширина и длина объема активной области соответственно.

Как и в инжекционных лазерах, с увеличением длины активной области поток генерируемого излучения вначале увеличивается, а затем стремится к постоянному пределу (см. §3.1). Мощность генерации, отнесенная к единице длины, имеет максимум, положение которого на графике Sr/l как функции Кг соответствует условию

/С.т=л/Р1(«в-/?)Р-Р= V<P-P- (5.25)

Коэффициент полезного действия равен отношению потоков генерируемого излучения к общему потоку возбуждения, падающему на переднюю грань пластины 5j(l r) с коэффициентом отражения на частоте v„, равным г:

Ц= iZ =r/c°(v)(l-r)X

SbwI

l-(S/c.)(l+-)

Kr/(Kr + p). (5.26)

При постоянном уровне возбуждения значение ц достигает максимума, когда параметры активной среды удовлетворяют условию (5.25). С ростом накачки КПД вначале увеличивается, а затем стремится к конечному пределу, равному (5.26) без слагаемого 1/Sb-O. Таким образом, в рамках рассмотренного приближения в выражения для порога, мощности и КПД генерации лазеров с оптической накачкой входят параметры р, Pi, So, гг=1-Y и а. Эти же параметры определяют оптимальный режим генерации и максимальный КПД. Первые четыре параметра аналогичны внутренним параметрам инжекционных лазеров. Параметр нелинейности а для