
 |
|
Главная Усиленная люминесценция [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [ 34 ] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] бодные носители в свою очередь становятся источником возбуждения кристалла. Следовательно, один высокоэнергетический электрон рождает в веществе электронную лавину. Одновременно испускаются рентгеновские лучи, оптическое излучение и не менее двух третьих энергии первичного электрона превращается в тепло. Энергия электронов, используемых для возбуждения генерации, как правило, заключена в пределах 10... ...300 кэВ. Нижняя граница обусловлена необходимостью создания инверсной населенности в слое достаточной толщины. Если £е<10 кэВ, то возбуждается слишком тонкий приповерхностный слой вещества, велики дифракционные потери излучения, а на поверхности обычно имеется большое число дефектов, снижающих квантовый выход люминесценции и повышающих порог. Минимальное значение Ее, при котором получена малоэффективная генерация, равно 5 кэВ. Верхняя граница для Ее совпадает с порогом образования радиационных дефектов, повышающих порог и снижающих мощность генерации, а также ведущих к быстрой деградации лазера. В фосфиде индия атом фосфора смещается из узла решетки в междоузлие под действием электронов с энергией ПО кэВ. Чтобы выбирать атомы мышьяка и селена со своих мест в кристаллах арсенида галлия и селенида индия, требуются энергии электронов 273 кэВ и 325 кэВ соответственно (рис. 6.1). При этом глубина проникновения электронов в кристалл не превышает 100 мкм. , Простраиственное распределение возбужденных электронов и дырок. Важнейшей характеристикой пространственного распределения возбуждаемых носителей является глубина проникновения первичных электронов в кристалл. Она определяет толщину слоя активной среды. Хорошее согласие с опытом дает расчет глубины проникновения электронов на основании формулы Бете, характеризующей изменения энергии электронов на единице длины их пробега dEe/dr в результате ионизации атомов: dEe ZnueeZ nXeVl mevlEe 2/2(1-Pe) 1 -2(Vr- -1+P) In2+1-Pe4 4-(1-Vr) (6.1) InSeiSe)32i Cmd}299\ WO  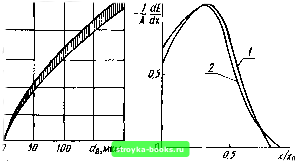 Рис. 6.1. Зависимость глубины проникновения электронов rfe от их энергии £е- Слева указаны пороги образования радиационных дефектов, в скобках - смещаемые атомы Р и С. 6.2. Распределение ионизационных потерь по глубине кристалла германия: £„ = 50 кэВ (/) и .500 кэВ (2). Кривая 2- график функции (6.2) где Пе - число связанных электронов в единице объема кристалла; Z - атомный номер; Ше - масса электрона; / - средняя энергия ионизации атома; Ре - отношение скорости электрона к скорости света. При сравнении экспериментальных кривых с теоретическими для легких (Z<;15) и тяжелых (Z> 15) элементов необходимо брать значения /, равные 11,5Z эВ и 9Z эВ соответственно. Приближенно распределение плотности потерь энергии электронов на ионизацию можно представить формулой л-<-)v* (6.2) Нормировочный множитель А выбирается таким, чтобы максимальное значение -dE/dx, приходящееся на точку х = а, было равно единице. Параметр b находится из сравнения кривой (6.2) с результатом точных расчетов или из сравнения с экспериментальными кривыми. Результаты численных расчетов на ЭВМ ионизационных потерь в германии, соответствующих экспериментальным данным, и график функции 6.2) приведены на рис. 6.2. По оси ординат отложена безразмерная глубина проникновения электронов х/хо, где - полная (спрямленная) длина пробега электрона в веществе. В этих координатах кривые -dE/dx, рассчитанные для начальных энергий электронов £0 = 50 эВ и 500 эВ, и график (6.2) практически совпадают. Для £о в интервале 50...200 кэВ зависимость хо от начальной энергии электронов можно выразить формулой Хо = С lEo -\- С2Е0. Если энергию электронов выражать в килоэлектронвольтах, то для арсенида галлия и сульфида кадмия коэффициенты пропорциональности С, = 0,116 мкм/кэВ, С2 = 2,7-10- мкм/кэВ1 Следовательно, в указанных пределах изменения £о полная глубина проникновения возрастает от 12,6 до 131 мкм. В результате каскадных процессов рассеяния первичные и вторичные электроны будут не только проникать в глубь кристалла, но и распространяться по всем другим направлениям. Область возбуждения может быть значительно шире, чем сечение пучка быстрых электронов, падающих на поверхность образца. Достаточно полной характеристикой пространственного распределения возбуждаемых носителей могут служить поверхности равного уровня возбуждения или поверхности потерь равной плотности. Сечение таких поверхностей плоскостью, перпендикулярной к поверхности кристалла, показано на рис. 6.3. Видно, что распространение электронов в боковых направлениях по величине сравнимо с глубиной их проникновения в кристалл. Легко представить, как будут деформироваться кривые на рисунке, если увеличивать диаметр пучка возбуждающих электронов. Очевидно, что по краям пучка сохранится размытие, аналогичное дифракции света, пропускаемого через круглое отверстие, а в центральных областях кривые пойдут параллельно поверхности кристалла, но и в этом случае сохраняется крайне неоднородное возбуждение среды по глубине. Чтобы перейти от величины потерь энергии электронов к концентрации свободных носителей, необходимо учесть, что для образования одной электронно-дырочной пары требуется энергия, примерно равная 3£g. В арсениде галлия £g~l,5 эВ и в области кривой с цифрой 1000 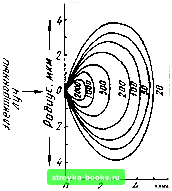 Рис. 6.3. Кривые ионизационных потерь равной плотности в GaAs, возбуждаемом бесконечно тонким лучом с энергией электронов 30 кэВ. Цифры около кривых плотности потерь выражены в эВ/мкм.электрон на рис. 6.3 один электрон с энергией 30 кэВ создает концентрацию свободных носителей, равную ;6,7-10 мкм- = 6,7-10 см Чтобы получить инверсную населенность, соответствующую п=10* см, требуется 1,5-10 электронов. Поперечное и продольное возбуждение. Конструкции лазеров с электронной накачкой создаются с учетом нескольких ограничительных факторов. Во-первых, энергия быстрых электронов ограничена сверху порогом образования радиационных дефектов. Следовательно, глубина их проникновения также ограничена несколькими десятками микрометров. Размеры активной среды в направлении распространения электронов всегда остаются относительно небольшими, как при однофотонном возбуждении в лазерах с оптической накачкой. Во-вторых, поскольку более двух третьих энергии накачки превращается в тепло, то возбуждаемый слой быстро нагревается. Требуется либо импульсное возбуждение, либо хороший теплоотвод при непрерывной накачке. В-третьих, плотность потока генерируемого излучения ограничена сверху порогом разрушения зеркал резонатора (см. §5.1). Кроме того, как и в лазерах всех других типов, размеры активной области в плоскости, перпендикулярной к оси резонатора, ограничены из-за усиленной люминесценции (спонтанного шума), препятствующей созданию требуемого уровня инверсной населенности. 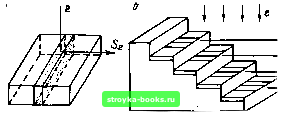 e Рис. 6.4. Полупроводниковые лазеры с электронной накачкой: а - активная среда между двумя пластинами из сапфира; 6 - многоэлементный лазер с поперечным возбуждением; s - многоэлементный лазер с продольным возбуждением и выносным зеркалом; г--лазер с распределенной обратной связью; - лазер с неустойчивым генератором Подобно лазерам с оптической накачкой (см. рис. 5.1) применяются поперечный и продольный варианты возбуж-.дения электронным лучом. Для увеличения теплоотвода активная среда помещается между двумя сапфировыми пластинами, прикрепленными к хладопроводу (рис. 6.4, а). Второй способ избежать перегрева активной среды - это сканирование электронным лучом по поверхности пластины. Оно позволяет также перестраивать длину волны генерации, если имеется зависимость ширины запрещенной зоны от координаты, или создавать изображение, как в лазерных телевизионных трубках - кван-тоскопах. С целью получения мощного лазерного луча применяются многоэлементные лазеры. Обычно на полупроводниковой пластине делаются продольные и поперечные канавки, заполненные веществом, поглощающим усиленную люминесценцию (см. рис. 6.4, а, б). В резонаторе с выносным зеркалом за счет расходимости излучения может установиться оптическая связь между элементами, что приводит к уменьшению расходимости и повышению степени когерентности лазерного луча. На рис. 6.4, г показан лазер с распределенной обратной связью на основе арсенида галлия (Ю. А. Коэлов- ский, И. Г. Гончаров, К. Б. Дедюшко и др., 1975 г.). На тонкой пластине / из ;t?-GaAs, укрепленной на хладо-проводе 2, создавалась дифракционная решетка 3 методом травления через фоторезистивную маску. При толщине активной области 0,8 мкм глубина канавок достигала 0,1 мкм. Для вывода излучения использовалось зеркало. Чтобы получить однородное ближнее поле генерации, применяются неустойчивые резонаторы (рис. 6.4, д). В таком резонаторе одно из зеркал вогнутое, что резко увеличивает потери для аксиальных и неаксиальных мод. Резонатор становится селективным для различных типов колебаний. Это обеспечивает возможность получить генерации на одной из неаксиальных мод. Если в плоском резонаторе ближнее поле имеет вид отдельных точек, то в неустойчивом резонаторе наблюдалось равномерное свечение по всему зеркалу. Для практических целей удобны лазеры в виде электронно-лучевых отпаянных трубок, в которых заключены и источник возбуждения, и активное вещество. § 6.2. ПОРОГОВЫЕ ХАРАКТЕРИСТИКИ Зависимость плотности порогового тока от энергии электронов. Концентрация свободных носителей, возбуждаемых быстрыми электронами, пропорциональна функции (6.1) и приближенно может быть выражена формулой Этой формулой можно пользоваться для стационарного или квазистационарного возбуждения, если длительность импульса накачки At больше то - времени жизни свободных носителей. При п(х) =Пп{х) = const, где Па{х) - пороговое значение концентрации, с увеличением значения Ео выражение в скобках также будет расти, а пороговый ток - уменьшаться. Однако п„(х) в принципе само является функцией Ео. Во-первых, с ростом энергии электронов увеличивается глубина их проникновения в кристалл, а следовательно, и толщина активной области. Поэтому уменьшаются дифракционные потери на зеркалах резонатора. Во-вторых, чем больше значение Ео, тем выше температура активной области, и заданный [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [ 34 ] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] 0.0008 |