
 |
|
Главная Усиленная люминесценция [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [ 39 ] [40] [41] [42] [43] [44] [45] [46] [47] [48] -------Ф- S,p.n 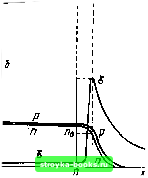 Рис. 7.5. Вид стримера, движущегося в направлении х(а); распределение напряженности поля и концентрации свободных носителей вблизи головки стримера (б) зующиеся за счет обратного пьезоэффекта с максимальной глубиной в направлениях фононной фокусировки, если константа электрон-фононного взаимодействия достаточно велика, противодействуют сверхзвуковому дрейфу свободных носителей в этом поле. Следовательно, в направлениях фононных струй электрическое поле будет возрастать до некоторой пороговой величины, обеспечивающей его отрыв от сферического поля и дальнейшее независимое продвижение импульса электрического поля по уже заданному направлению. Одновременно электрическое поле понижает симметрию кристалла, поэтому симметрия звезды стримеров не совпадает с симметрией кристаллической решетки до начала разряда. Встреча стримера с неоднородностью кристалла может привести к задержке стримера, а затем к новому пробою в направлениях фокусировки более медленных фононов. Теория Чернозатонского правильно предсказывает многие (в полупроводниках пока не все) направления распространения пробоя в щелочно-галлоидных кристаллах, в ниобате лития, парателлурите и гексагональных полупроводниках. Из нее вытекает также зависимость направлений стримеров от температуры и напряженности электрического поля. Однако механизм распространения стримера после его возникновения не рассматривается, и причина его внутренней устойчивости остается неясной. Генерация свободных носителей. В работах И. Г. Басова, А. Г. Молчанова, Ю. М. Попова и др. предполагается, что уже сформировавшийся стример имеет форму сильно вытянутого параболоида вращения с радиусом кривизны переднего фронта го (рис. 7.5). Приближенно процесс генерации носителей при перемещении стримера в кристалле описывается уравнениями баланса для электронов и дырок и уравнениями Пуассона для электрического пробоя дп dt (7.1) = - div /"+ анУд« + /?т + /?и, =а„идП + /?т + /?н, -* 4л div -(Р -«). /=еПр,е#+е(£>е + £>А) Vn. Здесь /-вектор плотности электронного тока; - коэффициент ударной ионизации; Уд и р,е - дрейфовая скорость и подвижность электронов; е - диэлектрическая постоянная кристалла; /?т и /?„ - скорости образования электронно-дыр очных пар за счет туннелирования и фотоионизации соответственно; De и Da - коэффициенты диффузии для электронов и дырок. Дырочный ток как малая величина по сравнению с электронным током в широкозонных полупроводниках не учитывается. Уравнения (7.1) описывают распространение стримера как продвижение по кристаллу токопроводящей плазмы. Вследствие высокой проводимости плазмы величина электрического поля внутри стримера незначительна, а на головке стримера имеет импульс поля с максимальным значением if о. В уравнениях учитывается три механизма образования свободных носителей: ударная ионизация, туннелирование электронов из валентной зоны в зону проводимости в электрическом поле и фотоионизация. Источником фотонов при стримерном разряде служат тормозное излучение, люминесценция и генерация излучения. Путем решения уравнений установлено, что для создания в сульфиде кадмия при 7 = 80 К концентрации свободных носителей ло=10 см~ только за счет ударной ионизации напряженность электрического поля должна быть равной 9о = 7-10® В/см. При учете лишь тормозного излучения или только туннельного эффекта для "Wo получено соответственно 10 В/см и 5,5-10® В/см. Отсюда сделан вывод, что основным механизмом возбуждения свободных носителей в стримере является туннели-рование электронов из валентной зоны в зону проводимости в электрическом поле. Однако при получении указанного вывода наряду с многими другими допущениями предполагалась возможность использования результатов стационарной теории туннелирования. Очевидно, она применима только в случае, если т„мп> Тт, где т„мп - время действия импульса электрического поля на электрон; Тт = •ехр {nW/Elyeh - время туннелирования, а -постоянная кристаллической решетки в направлении ДляЗ= 5-10® В/см и параметров сульфида кадмия g = 2,4 эВ, mr = me«A(me-f тл)~ = 0,1бто находим Тт = 2,410 с, а время действия поля на электрон Тимп~ ~ 10~*...10" с. Поэтому туннельный механизм при стримерном разряде может не сработать, хотя в целом теория туннелирования имеет широкие границы применимости. С. В. Войтиковым разработана теория нетуннельного электрополевого возбуждения полупроводников сверхкороткими импульсами электрического поля. Рассматривалась некая ограниченная область бесконечно протяженного кристалла. Предполагалось, что в начальный момент времени (to= - оо) поле на эту область не действует. Импульс поля движется со скоростью Uc и в момент времени /»0 проходит через выделенную область, возбуждает ее и уходит дальше. Начальное i и конечное / состояния описываются детерминантами Хартри - Фока - Слэтера, составленными из функции Блоха. Возбуждение полупроводника описывается временным уравнением для оператора эволюции U{t, to) U{t,to) = \+ -j\dxU(t,x)(x), (7.2) n п, t(T)= X \ e{ra-v,t)dra - оператор взаимодействия (возмущения); - общее число электронов в валентной зоне в выделенной области; fjw - проекция радиуса-вектора /-го электрона на вектор Ус. Амплитуда вероятности перехода электрона из валентной зоны в зону проводимости (7.3) А,с{к,к)= lim a\U{tJo)\i), где к и к- волновые векторы электрона в валентной зоне и зоне проводимости соответственно. Квадрат модуля Avc(K, к) равен вероятности перехода. В первом приближении теории возмущений расчеты дают Л - г X б (Ki - Кх + G X) б [Ее (к)-Е„ (к) - -hvc{4-Ki + G) ] ir(/с -/С + G) (кI ехр (-Ш?) \к). (7.4) Здесь б - векторы обратной решетки; {к\ - щ -f Оц) - фурье-образ W{r\)\ индексами и ± отмечены параллельные и перпендикулярные к скорости стримера Vc составляющие векторов. Поскольку в выражение для А\е входят б-функции, то- вероятность переходов будет отлична от нуля при выполнении, в частности, условия Ки,= \Ее{к)-Е.(к)\1{к\-щ). (7.5) Вектор обратной решетки опущен, так как его прибавление к волновому вектору электрона дает физически эквивалентное состояние. На зонной диаграмме произведение hvc равно тангенсу угла наклона стрелки, соединяющей начальное и конечное состояния электрона (рис. 7.6). Этот угол рвен 90°, т. е. будут реализовываться вертикальные (Прямые) переходы, если Vc-oo. При всех конечных значениях скорости перемещения импульса поля он будет меньше 90°. 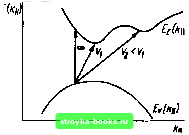 Рис. 7.6. Непрямые переходы без участия третьих частиц под действием ультракороткого импульса электрического поля Следовательно, при нетуннельном механизме возбуждения реализуется новый тип квантовых переходов, а именно: непрямые переходы без участия третьих частиц. Чем меньше скорость движения поля, тем больше наклон (отклонение от вертикали) стрелки, соединяющей начальное и конечное квантовые состояния. Из (7.2) и (7.4) следует также, что вероятность перехода растет пропорционально квадрату напряженности электрического поля. Это аналогично оптическому возбуждению, при котором вероятность вынужденного перехода Ви (см. § 1.1) прямо пропорциональна плотности энергии или квадрату амплитуды электрического вектора световой волны. Эффективность ионизации полупроводника электрическим полем зависит не только от амплитуды и скорости его перемещения, но и от формы импульса поля. Это хорошо видно из рис. 7.7, на котором приведены графики концентрации свободных носителей в сульфиде кадмия, возбуждаемом импульсами поля, имеющими форму прямоугольника, трапеции, треугольника и кривой cos (лГ)/2А/), где А/- пространственная ширина импульса. При расчетах брались следующие значения параметров: эффективные массы ml = m = 0,204то, т1 = 5то, m=0,7mo; £ = 2,4 эВ, сила осциллятора fvc=4; амплитуда поля =2-10 В/см; А/=10~ см. В случае / концентрация свободных носителей превышает 10 см~. Как только передний фронт импульса поля становится более пологим, эффективность возбуждения падает на порядок. Это падение продолжается с переходом к случаям 3 и 4 (см. рис. 7.7), так как крутизна переднего фронта уменьшается. Полученные результаты для закономерностей нетуннельного возбуждения качественно согласуются с экспе- 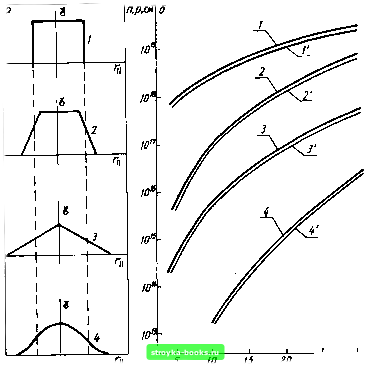 Рис. 7.7. Формы импульсов электрического поля (а) и соответствующие им концентрации возбужденных электронов и дырок как функции скорости импульса в CdS (б); /, 2,3,4 - вектор Vc перпендикулярен к оптической оси G; 1, 2, 3, 4 - Vc\\C риментальными данными по возбуждению стримеров и с общими выводами квантовой теории рассеяния, согласно которой эффективность взаимодействия частицы с потенциальным барьером увеличивается с повышением крутизны барьера. В таких быстропротекающих процессах, как стримерный разряд, диффузия носителей, по-видимому, не играет существенной роли. Стримеры в полупроводниках - кооперативные самоорганизованные процессы. Один из наиболее общих законов природы - второе начало термодинамики - в формулировке Р. Клаузиуса гласит: в замкнутой системе энтропия либо остается постоянной (в случае обратимых процессов), либо возрастает, если имеются необратимые [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [ 39 ] [40] [41] [42] [43] [44] [45] [46] [47] [48] 0.0009 |