
 |
|
Главная Усиленная люминесценция [0] [1] [2] [3] [4] [5] [ 6 ] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] Лазерная спектроскопия в состоянии экспериментально решать вопросы, связанные с неравновесным распределением носителей в зонах. Как правило, эти явления наблюдаются при возбуждении полупроводников сверхмощными ультракороткими импульсами лазерного излучения. Условия создания инверсной населенности. Рассмотрим условия инверсной населенности для двух дискретных уровней и модели параболических зон, типичной для межзонных переходов в полупроводниках. Коэффициент поглощения при квантовых переходах между двумя уровнями в максимуме спектральной линии к {Vii) {Bjinj - Bijni)hvij = (.-f»,). Эту формулу легко получить из дифференциального закона Бугера (1.2), если учесть, что ослабление света в слое и есть мощность поглощения этого слоя W„{vii), т. е. dS = -K ( v,,) Sijdx = - ir„ (v,;) dx, a плотность светового потока Sij = VgUii, где Vg - групповая скорость света в среде. Мощность поглощения в единице объема равна произведению числа поглощенных квантов (семь) на энергию одного кванта излучения: 44}-iBiin;-Biini). (1.26) Спектральная ширина линии Av,, появляется в формуле (1.25) как результат приближенного вычисления интеграла (1.24). По определению, инверсной населенностью называется такое распределение частиц по уровням, при котором коэффициент поглощения становится отрицательным. Полагая в (1.25) k(v,7)<0, снова находим условие инверсной населенности пары уровней: [1.27) Если степени вырождения уровней равны, то инверсная населенность реализуется, когда на верхнем уровне частиц будет больше, чем на нижнем.
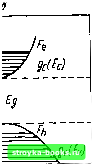 Рис. 1.2. Модель параболических Зои: о - зоны энергни; б - зависимость энергии электрона от волнового вектора к: в - зависимость плотности состояний в зонах от энергни В полупроводниках имеются широкие разрешенные и запрещенные зоны энергии, примесные уровни (примесные зоны). В оптических явлениях невырожденных полупроводников наиболее важную роль играют квантовые переходы вблизи экстремальных точек зонной структуры. Эти области можно аппроксимировать моделью -параболических зон (рис. 1.2). Уровни энергии в валентной зоне обозначим £„, в зоне проводимости - Ее, ширину запрещенной зоны - Eg. Функции плотности состояний соответственно gv{Ev) и gc{Ec). Пусть реализуются только прямые оптические переходы, когда волновой вектор электрона сохраняется: кжк. Обозначая коэффициент поглощения при межзонных переходах и отсутствии возбуждения x(v), для возбужденной системы будем иметь K(v)=x(v) [h{Ev)-UEc)]. Здесь (1.28) UE.) = g(£.-F.)/*r J lE,~F.)/kT (1.29) - функции Ферми - Дирака, описывающие распределение электронов в валентной зоне и зоне проводимости Ec - E = hv\ fe и - квазиуровни Ферми для электронов и дырок соответственно. Если общее число электронов в зоне проводимости равно п, а дырок в валентной зоне - р, то значения квазиуровней Ферми определяются из условий n=]gc{Ec)h{Ec)dEc, Р= i g4£.)[l-/e(£«)]d£„, - оо где Есо и Ем - энергии дна зоны проводимости и потолка валентной зоны соответственно (см. рис. 1.2). Согласно (1.28) x(v) равно значению коэффициента поглощения при условии, что все состояния в валентной зоне заняты, а в зоне проводимости свободны, т. е. /е(£ч) = 1, !г{Ес) =0. В (1.28) предполагается, что хотя в целом квантово-механическая система выведена из состояния термодинамического равновесия, в отдельных зонах устанавливается равновесное распределение электронов, описываемое функциями (1.29). Это предположение выполняется в широких пределах, в том числе и при возбуждении полупроводников сверхкороткими лазерными импульсами, поскольку времена релаксации в зонах равны (10- ... 10-") с. Из условия k(v) <0 с помощью (1.28), (1.29) находим условие инверсной населенности для полупроводников на частоте v: \F = Fe-F,>hv. (1.30) Чтобы излучение в полупроводниковом монокристалле усиливалось, расстояние между уровнями Ферми для электронов и дырок должно быть больше энергии кванта света /iv. Чем меньше частота, тем при меньшем уровне возбуждения-достигается инверсная населенность. В пределе условие (1.30) переходит в неравенство F>Eg. (1.30а) Для наблюдения усиления на опыте отрицательное значение должно превышать положительное значение коэффициента рассеяния p(v), т. е. должно выполняться неравенство k(v) +p(v) <0. § 1.2. НАКАЧКА Разновидности накачки. Процесс возбуждения лазерного вещества, приводящий к возникновению лазерной активной среды, называется накачкой лазера. В лазерной технике основными видами накачек являются: оптическая накачка; электрический разряд в газах; инжекция тока через р - п-переход, гетеропереход или поверхностно-барьерную структуру; возбуждение пучком быстрых электронов; электрический пробой полупроводников (стримерное возбуждение); быстропротекающие химические реакции, создающие продукты в возбужденном состоянии. Для возбуждения генерации в рентгеновской области спектра используется энергия взрыва атомных бомб. Универсальным способом создания инверсной населенности является оптическая накачка. Она позволяет возбуждать вещество в любом агрегатном состоянии во всех спектральных диапазонах. Для твердотельных (рубин, неодимовое стекло и т. д.) и жидкостных лазеров она ничем не заменима. Созданы газовые и полупроводниковые лазеры с оптической накачкой. В качестве источников излучения для накачки используются чаще всего лампы-вспышки и лазеры. Рубиновый лазер миниатюрных размеров можно возбуждать сфокусированным солнечным светом. Совокупность светодио-дов используется для возбуждения твердотельных лазеров. Активное вещество газовых лазеров характеризуется узкими линиями поглощения. Поэтому возбуждение их широкополосным излучением ламп-вспышек неэффективно. Для этих целей целесообразнее, хотя и не экономично, использовать лазерное излучение. Насыщение поглощения в системах с дискретными уровнями энергии. Для оптической накачки используются мощные потоки когерентного и некогерентного излучений, под действием которых возможно просветление вещества и насыщение поглощения, что сказывается на пороге и мощности генерации. Поэтому необходимо установить закономерность этого процесса. Первую формулу, дающую зависимость коэффициента поглощения от плотности потока излучения, получили Р. Карплус и Д. Швингер в 1948 г., рассмотревшие в рамках квантовой механики взаимодействие света с двухуровневой системой. Она имеет вид /с= , , , (1.31) 1 +const5 где 5 - плотность светового потока. Аналогичное выражение, но с учетом фона теплового излучения для системы частиц с двумя уровнями энергии, получено Б. И. Степановым. Покажем *\ что формула (1.31) справедлива для системы частиц с произвольным числом уровней энергии, если возбуждающее излучение изотропно. Для линейно поляризованного или не поляризованного, но направленного излучения справедливы другие формулы. Пусть имеется совокупность л жестко закрепленных частиц, каждая из которых обладает сколь угодно большим числом N уровней энергии. Частицы взаимодействуют с внешней радиацией, планковским излучением и окружающей средой. На возбуждающий свет не накладывается никаких ограничений, кроме тех, которые вытекают из условий применимости вероятностного метода расчета. Иногда его называют еще методом скоростных уравнений или уравнений баланса. В общем случае вероятности квантовых переходов между уровнями i и / равны р,; = Л, + В,У(у,,)+йо + Рф P;, = B,«»(v,-,)+d;,+p),. (1.32) Здесь dij и dji - вероятности неоптических переходов; Pi= (Si/Si)pih Pr, выражается интегралом (1.24). Угловую зависимость вероятности перехода удобно выразить с помощью четырех углов й, ф, , т),, (рис. 1.3). Углы ф определяют ориентацию некоторого фиксированного дипольного момента Dmi\ I - угол между матричными элементами и Dmi\ угол т),; дает положение вектора Оц на поверхности конуса, осью которого служит вектор Dml- Если совокупность частиц в целом образует изотропную систему, то число частиц, векторы которых Di лежат в пределах углов + ф-Ьф + Ф, а векторы Д,- в интервале от щ до +d, равно dQ dri 4rt 2л n sin ffdMffdr\ij. * Излагаемый здесь метод расчета был развит в долазериый период (1957-1960 гг.) в работах автора. См. сноску иа стр. 45. 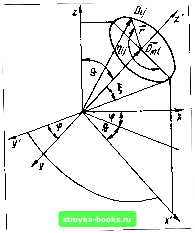 Рис. 1.3. Ориентация матричных элементов дипольного момента для переходов и i-l Эти частицы находятся в тождественных условиях по отношению к возбуждающему свету. Все вероятности переходов у них одинаковы, поэтому при стационарном режиме облучения справедлива следующая система кинетических уравнений: =-.,.(Q)Xa7 + + rt/p„ = 0, /= I, 2, 3, ... ,N, ij. (1.33) Так как общее число частиц неизменно, а их повороты отсутствуют, то в расчете на единичный телесный угол О, и единицу угла т],; имеем равенство (1.34) Следовательно, из N уравнений системы (1.33) линейно независимых будет только Л/ -1. Подставляя Hn из (1.34) в (1.33) и отбрасывая Л/-е уравнение, находим (1.35) [0] [1] [2] [3] [4] [5] [ 6 ] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] 0.0009 |
|||||||||||||||||