неправильно сконструированном входе форма изделия искала, ется.

Существенное влияние на качество оказывает систем нагрева и терморегулирования; она включает нагреватели цилиндра и головки экструдера с приборами контроля и р. гулирования, систем охлаждения цилиндра, червяка и загрузоч, ной зоны. Для некоторых материалов требуется особо точное поддержание температуры; современные системы позволяют обеспечить отклонение в пределах не более +1° С. Охлаждение загрузочной зоны необходимо для обеспечения стабильной подачи гранул из загрузочного бункера в цилиндр экструдера. Охлаждение червяка и цилиндра необходимо как для умень-шения инерционности работы нагревателей, так и для отвода излищнего тепла, выделяющегося из-за внутреннего трения в полимере; в ряде случаев охлаждение червяка позволяет оптимизировать режимы переработки. Для обеспечения необходимого качества существенны не только температура расплава, но и профиль изменения температуры в экструдере.

Следуюнщми важными параметрами технологического процесса являются линейная скорость и режим охлаждения. При изготовлении изоляции и оболочки методом экструзии скоросп) процесса обычно ограничивается не производительностью экструдера, а либо условиями охлаждения, либо сдвиговыми напряжениями, развиваемыми в матрице. В следующих параграфах рассмотрены примеры выбора оптимальных значений рассмотренных параметров. Ш

5.2. ОСНОВНЫЕ СВЕДЕНИЯ О РЕОЛОГИЧЕСКИХ СВОЙСТВАХ ц РАСПЛАВОВ ПОЛИМЕРОВ

Поскольку процесс переработки расплавов полимеров неизбежно связан с течением расплавов под воздействием различных сил, вызывающих в нем упругие, высокоэластические (зави-сянще от времени) и пластические (необратимые) деформации, то для исследования таких систем необходимо привлекать реологию, которая изучает закономерности деформации и течения в материалах под воздействием механических напряжений Под воздействием приложенного гидростатического давления расплав перемещается в направлении X от большего давления к меньшему, при этом скорость перемещения vx зависит ох координаты Y, перпендикулярной направлению скорости fx-у стенок канала скорость слоев равна скорости стенки (т.е. около неподвижной стенки скорость равна нулю) и увеличивается по мере удаления от нее. Перемещение слоев жидкости относительно друг друга происходит под воздействием напряжения сдвига т. Градиент скорости называют скоростЫ" сдвига y = dvx/dY. Между напряжением и скоростью сдвйГ 122

установившемся ламинарном течении существует следу-ошая взаимосвязь:

х=-цГ, (5.1)

где Л-величина, зависящая от вязкости жидкости, а л зависит свойств жидкости. При «=1 уравнение (5.1) представляет собой уравнение Ньютона, где т) - динамическая вязкость.

Для ньютоновских жидкостей х прямо пропорционально л а Я зависит только от температуры и не зависит от условий течения. Строго говоря, к ньютоновским относятся только низкомолекулярные жидкости, а расплавы полимеров, течение которых сопровождается сложными взаимодействиями как между макромолекулами, так и между надмолекулярными образованиями, характеризуются большей или меньшей зависимостью вязкости от скорости сдвига (аномалией вязкости), у таких полимеров, как полиамиды, полиэтилентерефталат, поликарбонат, аномалия вязкости выражена слабо {пхЦ. В то же время у расплавов полиэтилена, пластифицированного поливинилхлорида и других наблюдается сильная зависимость ц от Y, "ри этом т) уменьшается с увеличением у, т.е. л> 1.

Для практических расчетов вводят понятие эффективной вязкости и эффективной скорости сдвига, значение которых несложно получить экспериментально, например по данным полимерной вязкозиметрии. Из этих же данных определяют энергию активации вязкого течения Е, которая характеризует влияние температуры на вязкость по уравнению

Л=Ло"«". (5.2)

Чем выше энергия активации, тем сильнее влияет температура на вязкость. Значения Е (кДж/моль) для некоторых полимеров составляют:

При у=0 При i=IOc"

ПЭНП ............».......................................... 16 6

пэвп...................................................... 28 ю

ПВХ-пластикат........................................... 40 16

С увеличением давления р вязкость увеличивается примерно По закону Ti = Tioexp(P/j); для полиэтилена р = (1,2-;-1,4) -10* Па. Однако при дальнейшем увеличении давления в расплаве начинаются процессы, аналогичные кристаллизации, и вязкость резко возрастает. Критическое давление зависит от темпера-нуры. Оно составляет, например, для ПЭ 60 МПа при -)-150° С и 120 МПа при +165° С.

Таким образом, способность расплава течь характеризуют Ривыми течения, связывающими т, у, при различных Мпературах.

В качестве примера практического использования реологи- их данных рассмотрим установившийся ламинарный поток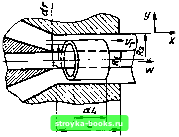

в формующей части матрицы при изготовлении кабельного из-делия (рис. 5.2), исходя из урав-нения (5.1) и полагая для про. стоты «=1. В потоке расплава выделим цилиндрический . элемент толщиной dr и длиной dL, движущийся в направлении X на расстоянии г от оси канала равномерно и прямолинейно со скоростью Vr- На этот элемент воздействуют следующие силы: перепад давления dp, действующий на площадь 2nrdr; напряжение сдвига т, создающееся на наружной поверхности элемента, равной 2n(r+dr)dL, и оказывающее тормозящее действие, а также напряжение сдвига, действующее на внутреннюю поверхность элемента InrdL. Суммируя действующие силы, получаем исходное уравнение:

dp Inrdr - т2я (г + dr)dL + T- InrdL = 0. (5.3)

После преобразования и интегрирования по г с учетом, что

=2-, получаем

Рис. 5.2. К расчету параметров в формующем канале матрицы

(5.4)

где Ci-постоянная интегрирования, определяемая из граничных условий, или с учетом (5.1)

(5.5)

Исходя из определения скорости сдвига и (5.5), запишем дифференщ1альное уравнение скорости

(5.6)

интегрируя которое по г, получаем скорость потока ва расстоянии г от оси канала

1 fpr

+ Ct In r+Cj

(5.7)

Объемный расход, определяемый из dQ = Vr2nrdr путем интегрирования, составляет

(5.1

Теперь по уравнениям (5.4)-(5.7), применяя соответствующие граничные условия и определяя Ci-С3, можно рассчитать основные параметры потока в любой точке матрицы. Для общего случая, показанного на рис. 5.1, граничные условия принимают ВИД при г = /?2 и Qr = Q (полная объемная производитель-

ность), а при г = Я D, = w (линейная скорость жилы). Заметим, что при w=0 получаем частный случай для потока в кольцевом канале, а при i?i=0-случай изготовления прутка. Опуская громоздкие промежуточные вычисления, учитывая, что на практике объемную производительность можно легко определить из равенства

Q = mw{Rl,„-Rl)K,

(5.9)

где 7?изд - наружный радиус готового изделия при +20° С, а т - коэффициент увеличения объема материала в матрице, равный отношению удельного объема материала при температуре экструзии к удельному объему при 4-20° С, и вводя обозначения

llnN

A={N-l)

получаем расчетные формулы для показателей процесса экструзии, приведенные в табл. 5.1. По приведенным формулам могут быть рассчитаны напряжение и скорость сдвига в любой точке сеченияформующего канала матрицы, их максимальные значения (у стенки матрицы), а также скорость потока в любой точке и объемная производительность.

Ниже приведены формулы для расчета максимальной скорости сдвига у для каналов различной формы при пф1:

Форма канала

Цилиндрическая Коническая .......

Щелевая {bxh).......................................................

Кольцевая................................................................ 2

Зп+Л Q п яЛ

In nR]Rl 2(2,1-1-1) Q

n bh 2И-Ц Q

n Jt(i?2-fi?i)(i?-i?J)

Отсюда нетрудно определить остальные параметры потока, например б и и, для цилиндрического канала:

2(/г-ьЗ)л/-"

иЧ-3 (jгГ->•"•) "~2--1(,Ц-1)~~;йг

(5.10)

(5.11)

Таблица 5.1. Расчетные формулы для пока»ателей процесса экструзии при различных условиях

выпрессоааяии

Продолжение табл. 5.1

Показатель

Скорость сдвига у.

Вид инструмента

для плотного наложения

7--5-гтг 2г----

rln/?2/i?l

rlnRi/R.

для свободного наложения (трубкой) для прутка

2\ r}aR2lRj

4rI-rJrI+rI-.3L)

\ In RilR J

Максимальная скорость сднига

-(В-1)

у RjlnRIRj

Напряжение ►3 сдвига т.

.4L\ rinRjIRj r\nR2lRi

Р 4L

Rl-Ri г In Л г/Л i