рице, внутри которых непрерывно движется изолируемая токопроводящая жила или полуфабрикат кабеля.

Расплав полимера фильтруется через сменный пакет метал-лических сеток, размещаемых между цилиндром и головкой. Повышение давления в головке обеспечивается с помощью решетки с отверстиями, разбивающей поток расплава полимера на много потоков меньшего сечения (по числу отверстий). Решетка находится непосредственно за сетками по направлению движения к головке. На конце червяка расположена насадка, назначение которой-способствовать более равномерному течению расплава полимера, исключающему образование застойных зон, в которых скорость движения расплава равна нулю. Как правило, насадка имеет на поверхности кольцевую нарезку. При вращении из-за сил трения червяк нагревается и поэтому охлаждается с помощью холодной дистиллированной воды, протекающей в его теле через трубки, расположенные в продольных проточках.

Так как полимер в различных зонах экструдера находится в различном состоянии и имеет различную плотность, то объем витков червяка в зоне / больше, чем в зоне III. Отношение этих объемов называется компрессией, или степенью сжатия, и количественно равно отношению плотности расплава к насыпной массе гранул. Компрессия в червяках для переработки пластмасс осуществляется, как правило, путем изменения глубины винтовой нарезки при постоянном по длине червяка шаге нарезки, а в червяках для переработки резиновых смесей чаще всего используется убывающий шаг нарезки. При выборке материалов для червяка стремятся к тому, чтобы сила трения между поверхностью червяка и расплавом полимера была минимальной, а между поверхностью червяка и втулкой цилиндра - максимальной.

Рассмотрим изменение давления по пути движения расплава вдоль оси червяка. Перерабатываемый материал при перемещении из зоны / в зоне / испытывает сопротивление продвиже-, нию, складывающееся в результате действия сил трения о стенки кольцевой нарезки и поверхность втулки цилиндра и сил сопротивления, оказываемых элементами головки (инструмент, сетки и т. д.). Поэтому, если на входе в цилиндр в зоне загрузки давление равно атмосферному, то в зоне III и в головке оно повышается в десятки раз. Увеличению давления по длине червяка способствует также наличие компрессии. Изменение давления вдоль оси чс-чяка показано на рис. 5.8.

При проведении расчетов, связанных с течением расплава полимера, как правило, пренебрегают изменением давления в зонах / и , принимая за противодавление Лр разность между давлением р2 на выходе в головку и давлением pi на

Рис. 5.8. Изменение давления вдоль оси червяка: - зоны: /-загрузки; И-переходная; Ш-дозирующая

входе в Зону /, которое в этом случае принимается равным атмосферному:

P=P2-Pi- (5.12)

С одной стороны, наличие противодавления снижает производительность экструдера, с другой-способствует получению более плотной и гомогенной изоляции, препятствует образованию в изоляции воздушных включений.

Расчет производительности Q экструдера основан на принципе наложения трех потоков расплава полимера в цилиндре, относящихся к единице времени: прямого Q„j,, обратного бобр и утечки Qy. Схема, приведенная на рис. 5.9, показывает направления этих потоков; на схеме приведены также обозначения, которые будут использованы в дальнейшем при выводе расчетных аналитических выражений [4].

Очевидно, что результирующий поток в единицу времени, или производительность экструдера, составит

Q=Qnp-Qoep-Qyr. (5.13)

прямой поток создается при вращении червяка и протекает 8 направлении скорости Vq, как это показано на схеме, братный поток направлен противоположно прямому потоку 51 возникает как следствие противодавления в цилиндре, фотиводавление создает и поток утечки, но этот поток "зникает в зазоре между гребнем нарезки червяка и втулкой

Рис. 5.9. Схема течения расплава в цилиндре экструдера

цилиндра, необходимом для свободного вращения червяка. Естественно, что фактически существует единый поток расплава Q, который движется от загрузочной воронки к головке, а обратный поток и поток утечки лишь уменьшают этот общий поток и, следовательно, сжимают производительность экструдера.

В общем случае течение жидкости описывается линейным дифференциальным уравнением Навье-Стокса:

grad р = цАу,

(5.14)

где р-локальное давление; ц-вязкость; v-вектор локальной скорости расплава полимера; Л - оператор Лапласа.

Если считать, что характер движения расплава полимера ламинарный, а сам расплав представляет собой несжимаемую изотропную жидкость, то для движения расплава по оси X со скоростью и, т. е. вдоль кольцевого канала червяка, уравнение (5.14) может быть представлено в следующей форме:

(5.15)

В представленной форме уравнение не требует, чтобы жидкость - расплав полимера - обладала ньютоновскими свойствами, а процесс был изотермичен. Это объясняется тем, что вязкость зависит от положения элемента жидкости в канале и определяется температурой и градиентом скорости в рассматриваемой точке. Однако решение уравнения в общем виде крайне затруднено, и поэтому делается ряд допущений, позволяющих в дальнейшем получить инженерные формулы для расчета производительности экструдера.

Учитывая, что вязкость расплава незначительно изменяется в поперечном сечении канала, т. е. д\х/дг=0, можно упростить (5.15) следующим образом: 136

SyJ By 8у

(5.16)

Далее, считая, что температура расплава по всей площади сечения постоянна (изотермический режим), можно предположить постоянство вязкости расплава по поперечному сечению

дх \dz дуЧ-

(5.17)

Кроме того, можно пренебречь изменением скорости течения по оси dvjdz = 0. Это полностью справедливо для червяков с малым отно1шением глубины нарезки к его ширине (А/6). Тогда dVx/dz = 0 или

дх-ду -д-дх -

Полученное выражение (5.18) относится к одномерному течению расплава в канале червяка, причем после сделанных допущений расплав должен рассматриваться как ньютоновская жидкость.

Как указывалось выше, в реальном экструдере изменение давления по длине дозирующей зоны принимается линейным. В этом случае

др ,Р Pi-Pi

дх Дх Z-a

где 1д-длина дозирующей зоны.

Следовательно, если обозначить как М, то

(1 Ах

ду ц Ал:

(5.19)

После двукратного интегрирования получаем

v = My/2 + Ay+B. (5.20)

Граничные условия, необходимые для определения постоян-ibix Л и В в (5.20), могут быть сформулированы следующим °Разом. Прежде всего условно примем, что червяк непо-ижен, а цилиндр вращается вокруг него в сторону, противоположную направлению червяка, при этом относительное Ремещение червяка, расплава полимера и цилиндра не "Меняется. Тогда при ; = 0 г. = 0, а при y = h v = Vo. Поэтому

В=0 и A = Vo/h-Mh/2. (5.21)

Рис. 5.10. Эпюры скоростей прямого, обратного и результирующего потоков

в канале червяка

1 А»

С учетом того, что =~д находим

(5.22)

В (5.22) первое слагаемое представляет собой скорость прямого потока, а второе-скорость обратного потока, при этом потоком утечки пренебрегаем.

Графически выражение (5.22) можно интерпретировать в виде эпюры скоростей, как это показано на рис. 5.10.

Для того чтобы выразить объемную производительность экструдера через параметры экструдера, прежде всего рассмотрим схему канала червяка с движущимся в нем потоком расплава (рис. 5.11).

Элементарный объемный расход материала в единиц) времени AQi или производительность в рамках элементарного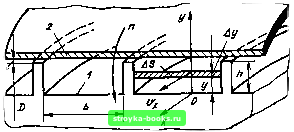

Рис. 5.11. Схема канала червяка с движущимся в ием\потоком расплав» 138

участка может быть выражена через скорость потока на ;,дементарном участке:

AQi = ViAS=v,bAy. (5.23)

рассматривая Q как lim Agj при л-+оо (Л-О) и переходя

1 = 1

к бесконечно малым приращениям, получаем:

С учетом (5.22)

ьфк bh dip

(5.24)

(5.25)

1 12ц Ах"

Далее выражаем Vq, Ь и Ар/Ах через параметры экструдера: частоту вращения п, диаметр червяка D, длину червяка I и параметры винтовой нарезки:

Vo=nDncos(p. (5.26)

Если обозначить расстояние вдоль оси червяка, соответствующее расстоянию Лл: по оси канала червяка, как А/, то

А/=Ал:8Шф и Ах = А 8Шф. Из анализа рис. 5.10 следует, что

6 = (а -6)со8ф и a = nDtg(p. Считая, что Ь<а, получаем

b = nDsin(p. С учетом (5.26)-(5.28) находим

(5.27)

(5.28) (5.29)

Q =- -h--

Вьфажение (5.29) не учитывает влияния потока утечки. С учетом потока утечки

=-2--щг А/-щы- -

Обозначим длину дозирующей зоны экструдера L12 и давление ассы соответственно в начале и конце дозирующей зоны " Pi и Pj. Тогда, считая, что давление увеличивается Начала дозирующей зоны, а в загрузочной и переходной онах давление равно атмосферному и изменение давления Постоянно по длине потока, получаем

(5.31) 139

Ap/Al={p2-py)/Li2-